Loi géométrique

Loi géométrique
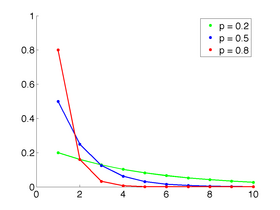Fonction de masse
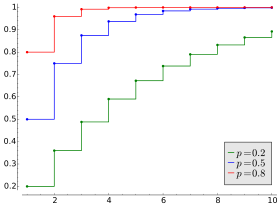Fonction de répartition
Paramètres	${\displaystyle p\in ]0;1[}$ ${\displaystyle q=1-p}$
Support	${\displaystyle k\in \mathbb {N} ^{*}}$
Fonction de masse	${\displaystyle q^{k-1}p}$
Fonction de répartition	${\displaystyle 1-q^{k}}$
Espérance	${\displaystyle {\frac {1}{p}}}$
Médiane	${\displaystyle \left\lceil {\frac {-\ln 2}{\ln q}}\right\rceil }$ (pas unique si ${\displaystyle {\ln 2}/{\ln q}\in \mathbb {Z} }$)
Mode	${\displaystyle 1}$
Variance	${\displaystyle {\frac {q}{p^{2}}}}$
Asymétrie	${\displaystyle {\frac {2-p}{\sqrt {q}}}}$
Kurtosis normalisé	${\displaystyle 6+{\frac {p^{2}}{q}}}$
Entropie	${\displaystyle {\frac {-q\log _{2}q-p\log _{2}p}{p}}}$
Fonction génératrice des moments	${\displaystyle {\frac {p\mathrm {e} ^{t}}{1-q\mathrm {e} ^{t}}}}$
Fonction caractéristique	${\displaystyle {\frac {p\mathrm {e} ^{\mathrm {i} t}}{1-q\mathrm {e} ^{\mathrm {i} t}}}}$
Fonction génératrice des probabilités	${\displaystyle {\frac {pt}{1-qt}}}$
modifier

En théorie des probabilités, la loi géométrique de paramètre ${\displaystyle p}$ peut désigner, selon la convention choisie, l'une des deux lois de probabilité suivantes :

• la loi de probabilité d'une variable aléatoire (v.a.) ${\displaystyle X}$ comptant le nombre d'épreuves de Bernoulli indépendantes de probabilité de succès p ∈ ]0,1[ nécessaires pour obtenir le premier succès. ${\displaystyle X}$ est la variable aléatoire donnant le rang du premier succès. Le support de la loi est alors {1, 2, 3, ...}.
• La loi d'une variable aléatoire (v.a.) ${\displaystyle Y}$ comptant le nombre d'échecs avant le premier succès dans une répétition d'épreuves de Bernoulli indépendantes de probabilité de succès ${\displaystyle p}$ Le support de la loi est alors {0, 1, 2, 3, ...}. On remarque que les variables aléatoires sont liées par la relation ${\displaystyle Y=X-1}$

Ces deux lois sont différentes. C'est pourquoi il faut préciser la convention choisie en indiquant le support.

Par la suite, sauf mention contraire, on considèrera que ${\displaystyle X}$ représente le rang du premier succès (le nombre d'épreuves effectuées dont celle réussie) et on notera ${\displaystyle q=1-p}$ la probabilité d'un échec dans l'épreuve de Bernoulli.

Exemples

• Supposons un dé équilibré à 6 faces. ${\displaystyle X}$ peut permettre de déterminer le nombre moyen de lancers nécessaire pour obtenir un 6. Ce nombre est l'espérance de la loi géométrique de paramètre ${\textstyle p={\frac {1}{6}}}$.
• Supposons une machine à vêtements démarrant à l'instant ${\displaystyle t_{0}}$ puis opérant aux instants ${\displaystyle t_{1}<t_{2}<t_{3}<\dots }$ En chaque instant la machine a une probabilité ${\textstyle p=0,002}$ de tomber en panne. ${\displaystyle Y}$ peut permettre de modéliser le temps de fonctionnement sans panne ${\textstyle T=t_{Y}-t_{0}}$.

Définition

Support sur les entiers strictement positifs

Soit ${\displaystyle q=1-p}$. Alors :

${\displaystyle \mathbb {P} (X=k)=q^{k-1}p\quad \forall k\in \mathbb {N} ^{*}}$

La probabilité ${\displaystyle \mathbb {P} (X=k)}$ correspond à la probabilité d'obtenir dans une succession de k épreuves de Bernoulli, k – 1 échecs suivis d'un succès. Les épreuves étant indépendantes, cette probabilité est de q^{k – 1}p. Dans la suite, nous prenons cette définition.

Support sur les entiers positifs

Pour l'autre définition, le nombre ${\displaystyle Y}$ d'échecs avant succès :

${\displaystyle \mathbb {P} (Y=k)=q^{k}p}$

${\displaystyle Y}$ n'est qu'un décalage de ${\displaystyle X}$. Son espérance n'est pas ${\textstyle {\frac {1}{p}}}$ mais ${\textstyle {\frac {1}{p}}-1={\frac {q}{p}}}$. En revanche, la variance est identique pour les deux définitions.

Modèle de durée de vie et loi exponentielle

Si on appelle ${\displaystyle p}$ la probabilité de désintégration d'une particule radioactive en chaque instant, la loi géométrique est le premier modèle discret de la mort d'une particule radioactive. La durée de vie de la particule radioactive ${\displaystyle V}$ suit la loi de probabilité suivante :

${\displaystyle \mathbb {P} (V=k)=q^{k-1}\quad \forall k\in \mathbb {N} ^{*}}$

${\displaystyle \mathbb {P} (V>k)=q^{k}=\mathrm {e} ^{k\ln q}}$

Si ${\displaystyle p}$ est petit, ${\displaystyle \ln(1-p)}$ est proche de ${\displaystyle -p}$. Donc

${\displaystyle \mathbb {P} (V>k)\approx \mathrm {e} ^{-kp}}$

On retrouve la distribution de la loi exponentielle.

Espérance, variance, écart type

L'espérance d'une variable aléatoire X suivant une loi géométrique de paramètre p est ¹⁄_p, et sa variance est q/p² où q = 1 – p est la probabilité d'échec :

$${\displaystyle \mathbb {E} [X]={\frac {1}{p}},\qquad \mathbb {V} [X]={\frac {1-p}{p^{2}}}={\frac {q}{p^{2}}}.}$$

L'écart type est donc √q/p.

Démonstration

Calculs préliminaires : pour tout x de [0, 1[,

$${\displaystyle {\begin{aligned}f(x)&=\sum _{k=0}^{+\infty }x^{k}={\frac {1}{1-x}}\\f^{\prime }(x)&=\sum _{k=1}^{+\infty }kx^{k-1}={\frac {1}{(1-x)^{2}}}\\f^{\prime \prime }(x)&=\sum _{k=2}^{+\infty }k(k-1)x^{k-2}={\frac {2}{(1-x)^{3}}}.\end{aligned}}}$$

En particulier :

$${\displaystyle {\begin{aligned}\sum _{k=1}^{+\infty }k^{2}x^{k-1}&=x\sum _{k=2}^{+\infty }k(k-1)x^{k-2}+\sum _{k=1}^{+\infty }kx^{k-1}\\&={\frac {2x}{(1-x)^{3}}}+{\frac {1}{(1-x)^{2}}}\\&={\frac {2}{(1-x)^{3}}}-{\frac {1}{(1-x)^{2}}}.\end{aligned}}}$$

On peut alors utiliser ces identités pour le calcul de l'espérance :

$${\displaystyle {\begin{aligned}\mathbb {E} (X)&=\sum _{k=1}^{+\infty }kq^{k-1}p\\&={\frac {p}{(1-q)^{2}}}\\&={\frac {1}{p}},\end{aligned}}}$$

car q = 1 – p, et pour celui de la variance :

$${\displaystyle {\begin{aligned}\mathrm {Var} (X)&=\left(\sum _{k=1}^{+\infty }k^{2}q^{k-1}p\right)-\mathbb {E} [\mathrm {X} ]^{2}\\&={\frac {2p}{(1-q)^{3}}}-{\frac {p}{(1-q)^{2}}}-{\frac {1}{p^{2}}}\\&={\frac {2}{p^{2}}}-{\frac {1}{p}}-{\frac {1}{p^{2}}}\\&={\frac {q}{p^{2}}},\end{aligned}}}$$

la première égalité ci-dessus provenant du théorème de König-Huygens.

Par exemple, pour ${\displaystyle p=1/2}$, ${\displaystyle \mathbb {E} [X]=2,\mathbb {V} [X]=2,\sigma [X]={\sqrt {2}}}$ et l'écart moyen ${\displaystyle {\textbf {EM}}(X)=\mathbb {E} (|X-2|)=\sum _{k=1}^{+\infty }{|k-2|/2^{k}}=1}$.

Liens avec d'autres lois

Lien avec la loi géométrique tronquée

Dans les programmes 2011 de Première Scientifique en France^[1], on appelle loi géométrique tronquée de paramètres n et p, la loi de la variable aléatoire obtenue en limitant à n le nombre d'épreuves de Bernoulli de paramètre p et en notant k le rang du premier succès. Par convention, s'il n'advient aucun succès au cours des n essais, on pose X = 0 (on trouve parfois pour X le nombre d'échecs consécutifs obtenus avant l'obtention d'un premier succès au cours des n épreuves^[2]). La probabilité que X = k est alors, pour k = 1, 2, 3, ..., n :

${\displaystyle \mathbb {P} (X=k)=q^{k-1}p}$

et pour k = 0

${\displaystyle \mathbb {P} (X=0)=q^{n}.}$

Cette loi de probabilité a pour espérance^[1]: ${\displaystyle \mathbb {E} (X)={\frac {1}{p}}\left(1-\left(np+1\right)q^{n}\right)}$ où q = 1 – p.

Le terme « tronquée », ici, n'a pas le même sens que celui que l'on trouve dans la définition d'une loi tronquée.

Lien avec la loi exponentielle

La loi géométrique est une version discrétisée de la loi exponentielle. En conséquence, la loi exponentielle est une limite de lois géométriques renormalisées.

Propriété — Si X suit la loi exponentielle d'espérance 1, et si ${\displaystyle Y=\lceil \theta X\rceil ,\ \theta >0,}$ alors Y suit la loi géométrique de paramètre

${\displaystyle p\ =\ 1-\mathrm {\mathrm {e} } ^{-\ {\tfrac {1}{\theta }}}.}$

Démonstration

${\displaystyle {\begin{aligned}\mathbb {P} (Y=k)&=\mathbb {P} (\lceil \theta X\rceil =k)\\&=\mathbb {P} (\theta X\in ]k-1,k])\\&=\mathbb {P} \left(X\in \left]{\tfrac {k-1}{\theta }},{\tfrac {k}{\theta }}\right]\right)\\&=F_{X}\left({\tfrac {k}{\theta }}\right)-F_{X}\left({\tfrac {k-1}{\theta }}\right)\\&=\exp \left(-\ {\tfrac {k-1}{\theta }}\right)-\exp \left(-\ {\tfrac {k}{\theta }}\right)\\&=\left(\mathrm {e} ^{-\ {\tfrac {1}{\theta }}}\right)^{k-1}\ \left(1-\mathrm {e} ^{-\ {\tfrac {1}{\theta }}}\right).\end{aligned}}}$

Notons que, pour un nombre réel x, ${\displaystyle \lceil x\rceil }$ désigne la partie entière supérieure de x, définie par

${\displaystyle \lceil x\rceil \ =\ \min \left\{k\in \mathbb {Z} \ |\ k\geqslant x\right\}.}$

Conséquence :

Ainsi, pour obtenir une variable aléatoire Y' suivant une loi géométrique de paramètre p arbitraire (avec toutefois la contrainte 0 < p < 1), à partir d'une variable aléatoire exponentielle X' de paramètre λ, il suffit de poser

${\displaystyle Y^{\prime }=\lceil \theta X^{\prime }\rceil ,}$

où l'on a choisi

${\displaystyle \theta \ =\ -{\tfrac {\lambda }{\ln \left(1-p\right)}}.}$

En effet, ${\displaystyle X=\lambda \,X^{\prime }}$ suit une loi exponentielle de paramètre 1 (et d'espérance 1).

Réciproquement,

Propriété — Si, pour ${\displaystyle n\geq 1,}$ la variable aléatoire Y_n suit la loi géométrique de paramètre p_n, et si, simultanément,

${\displaystyle \lim _{n}p_{n}\ =\ 0\qquad {\text{et}}\qquad \lim _{n}p_{n}/a_{n}\ =\ \lambda >0,}$

alors a_nY_n converge en loi vers la loi exponentielle de paramètre λ.

Démonstration

On se donne une variable aléatoire exponentielle X de paramètre 1, et on pose

${\displaystyle {\begin{aligned}\theta _{n}&=-{\tfrac {1}{\ln \left(1-p_{n}\right)}},\\\mathrm {Y} _{n}^{\prime }&=\lceil \theta _{n}\mathrm {X} \rceil .\end{aligned}}}$

Alors Y_n et ${\displaystyle Y_{n}^{\prime }}$ ont même loi, en vertu de la propriété précédente. Par ailleurs, pour tout ω

${\displaystyle \lim _{n}a_{n}Y_{n}^{\prime }(\omega )\ =\ \lim _{n}a_{n}\lceil \theta _{n}X(\omega )\rceil =\ \left(\lim _{n}a_{n}\theta _{n}\right)\ X(\omega )\ =\ X(\omega )/\lambda .}$

Or d'une part la convergence presque sûre entraine la convergence en loi, d'autre part la loi de X/λ est la loi exponentielle de paramètre λ.

Lien avec la loi binomiale négative

Si X_n est une variable aléatoire distribuée selon la loi binomiale négative de paramètres n et p, alors X_n a même loi que la somme de n variables aléatoires indépendantes distribuées selon une loi géométrique de paramètre p.

Voir aussi

• Variables aléatoires élémentaires
• Radioactivité
• Méthode de rejet
• Processus de Bernoulli
• Loi exponentielle
• Loi binomiale négative
• Problème du collectionneur de vignettes (un exemple faisant apparaître une loi géométrique)

Notes et références

• Portail des probabilités et de la statistique