Trajectoire d'un projectile

En physique, la trajectoire d'un projectile est le chemin que ce projectile empruntera après avoir été lancé.

Par projectile, on entend un objet petit et à masse réduite (par exemple un caillou ou un boulet de canon) par rapport à la taille et à la masse du corps depuis lequel il est propulsé (ce peut être la Terre, la Lune, etc.) à une vitesse et avec un angle tels qu'il ne puisse pas se maintenir en orbite et qu'il retombe. En outre, il faut que sa vitesse soit suffisamment faible par rapport à la vitesse de la lumière — que le facteur de Lorentz qui la caractérise soit suffisamment proche de 1 — pour ne pas devoir quitter les considérations de la physique classique.

Lorsque l’on étudie la trajectoire d’un projectile en négligeant toutes les forces à l'exception du poids, on parle de trajectoire balistique. La résolution des équations de la trajectoire balistique d'un projectile est aisée, mais cette modélisation est éloignée de la réalité lorsque d'autres forces sont considérées, par exemple les forces induites par le fluide dans lequel évolue le projectile (forces de frottement, poussée d'Archimède, etc.).

Notations

Dans les équations de l'article, les variables suivantes seront utilisées :

• g : l'accélération de la pesanteur en m/s² (9,81 m/s² à la surface de la Terre) ;
• θ ou α : l'angle de portée, c'est-à-dire l'angle avec lequel le projectile est lancé, en degrés ;
• v₀ ou v_i : la vitesse initiale, à laquelle le projectile est lancé, en m/s ;
• y₀ ou h : la hauteur initiale du projectile, en mètres ;
• d : la distance horizontale parcourue par le projectile, du point de lancement au point de tombée au sol, en mètres.
• k : le coefficient de proportionnalité caractéristique de la traînée du fluide.

Aussi, pour exprimer les distances, on pourra utiliser un repère cartésien orthonormé ${\displaystyle {\mathcal {R}}=(O;{\vec {i}},{\vec {j}},{\vec {k}})}$ où O est le point d'où est lancé le projectile. On appellera l'axe de coordonnées ${\displaystyle (Ox)=(O;{\vec {i}})}$ l'horizontale, l'axe de coordonnées ${\displaystyle (Oy)=(O;{\vec {j}})}$ la verticale, et l'axe de coordonnées ${\displaystyle (Oz)=(O;{\vec {k}})}$ la profondeur.

Trajectoire balistique

La trajectoire balistique d'un projectile est le chemin que prendra un projectile soumis à la seule action de la gravitation, en négligeant toutes les autres forces.

Équations horaires et cartésiennes

Distance parcourue

La distance horizontale totale d parcourue jusqu'à ce que le projectile retombe au sol est donnée par :

${\displaystyle d={\frac {v_{0}}{g}}\cos \alpha \left(v_{0}\sin \alpha +{\sqrt {(v_{0}\sin \alpha )^{2}+2gh}}\right).}$

Lorsque la hauteur initiale est égale à zéro, la distance parcourue se calcule ainsi :

${\displaystyle d={\frac {v_{0}^{2}}{g}}\sin \left(2\alpha \right).}$

Temps de vol

Le temps de vol t est le temps qu'il faut au projectile pour retomber au sol, soit le temps où on atteint ${\displaystyle x(t)=d}$:

${\displaystyle t={\frac {d}{v\cos \theta }}={\frac {v\sin \theta +{\sqrt {(v\sin \theta )^{2}+2gy_{0}}}}{g}}.}$

Hauteur maximale

La hauteur maximale h atteint par le projectile lors de son vol se calcule comme suit :

${\displaystyle h={\frac {v_{0}^{2}\sin ^{2}(\theta )}{2g}}}$.

Angle de portée pour atteindre une distance d

L'angle de portée est l'angle θ avec lequel un projectile doit être lancé dans le but de parcourir une distance d, compte tenu de la vitesse initiale v_0. La trajectoire étant parabolique, il est plus simple d'utiliser les propriétés de symétrie de la trajectoire et donc que la hauteur maximale est atteinte à la moitié du parcours, donc

${\displaystyle {\frac {v_{0}^{2}\sin(2\theta )}{2g}}={\frac {d}{2}}}$

${\displaystyle \sin(2\theta )={\frac {gd}{v_{0}^{2}}}}$

donc :

${\displaystyle \theta ={\frac {1}{2}}\arcsin \left({\frac {gd}{v_{0}^{2}}}\right)}$

ou

${\displaystyle \theta ={\frac {\pi }{2}}-{\frac {1}{2}}\arcsin \left({\frac {gd}{v^{2}}}\right)}$

Vitesse à une distance x

La valeur absolue |v| de la vitesse du projectile à une distance x est donnée par :

${\displaystyle |v|={\sqrt {v^{2}-2gx\tan \theta +\left({\frac {gx}{v\cos \theta }}\right)^{2}}}.}$

Angle θ nécessaire pour atteindre les coordonnées (x ; y)

Pour atteindre une cible à distance x et une altitude y lorsque le projectile est lancé du point de coordonnées (0 ; 0) à une vitesse v, les valeurs de l'angle de portée θ se calculent ainsi :

${\displaystyle \theta =\arctan {\left({\frac {v^{2}\pm {\sqrt {v^{4}-g(gx^{2}+2yv^{2})}}}{gx}}\right)}.}$

Trajectoire d'un projectile évoluant dans un fluide

Lorsqu'un projectile évolue dans un fluide, il subit une force de traînée qui s'oppose à son mouvement. Cette force de traînée est caractéristique de la forme du projectile, de sa vitesse, et des caractéristiques du fluide.

La traînée est un objet d'étude de la mécanique des fluides, qui ne considère plus le mouvement du mobile dans le fluide, mais qui suppose le mobile fixe et s'intéresse alors à l'écoulement du fluide autour de celui-ci. Cet écoulement est souvent complexe, et est caractérisé par un nombre sans dimension, appelé nombre de Reynolds et noté ${\displaystyle \mathrm {R_{e}} }$ :

${\displaystyle \mathrm {R_{e}} ={\frac {v\,L\,\rho }{\eta }}}$ avec v la vitesse relative du fluide en mètre par seconde, L la taille caractéristique de l’écoulement en mètres, ρ la masse volumique du fluide en kilogrammes par mètre cube, et η la viscosité dynamique du fluide en pascal-seconde.

On sait alors par l'expérience que^[1] :

• lorsque ${\displaystyle \mathrm {R_{e}} <\!\!<1}$ (il s'agit d'un écoulement de Stokes), la traînée est proportionnelle à la vitesse du mobile : le frottement que subit le projectile est dit linéaire ;
• lorsque ${\displaystyle 30<\mathrm {R_{e}} <800}$ (l'écoulement est laminaire), la traînée est approximativement proportionnelle à la vitesse du mobile à la puissance 1,4 ;
• lorsque ${\displaystyle \mathrm {R_{e}} >2000}$ (l'écoulement est turbulent), la traînée est proportionnelle au carré de la vitesse du mobile : le frottement que subit le projectile est dit quadratique.

On modélisera la traînée comme étant proportionnelle à la vitesse du projectile élevée à une puissance λ :

${\displaystyle F_{T}=-k\ v^{\lambda }\quad }$ avec F_T la force traînée du fluide en newtons, v la vitesse du projectile, et k le coefficient de proportionnalité caractéristique de la traînée qui s'exprime en kilogrammes par seconde

en prenant en compte la poussée d'Archimède, qui pousse le projectile dans le sens contraire au champ de pesanteur, d'autant plus que son volume est grand et que la masse volumique du fluide et l'intensité de son champ de pesanteur sont importants :

${\displaystyle {\vec {P_{A}}}=-\rho \,V\,{\vec {g}}\quad }$ avec ρ la masse volumique du fluide en kilogrammes par mètre cube et V le volume du projectile en mètres cubes.

Approximation par analyse numérique

On suppose dans cette section que l’évolution de la vitesse se fait par approximation sur la tangente au point initial (méthode d'Euler). En procédant pas à pas, avec un pas très petit, cette solution est extrêmement satisfaisante, d’autant plus qu’il est très facile de la mettre en œuvre avec un ordinateur.

Avec γ le facteur de précision, c'est-à-dire le facteur qui définit la durée d'une unité de temps, ainsi qu'avec v_i la vitesse initiale (en m/s) du projectile, son angle de portée α (en radians) et sa hauteur initiale h (en mètres), on a :

${\displaystyle x\left(t+1\right)=x\left(t\right)+v_{x}\left(t\right)\gamma \quad {\text{ avec }}\quad x\left(0\right)=0}$

${\displaystyle y\left(t+1\right)=y\left(t\right)+v_{y}\left(t\right)\gamma \quad {\text{ avec }}\quad y\left(0\right)=h}$

${\displaystyle v_{x}\left(t\right)=v_{x}\left(t-1\right)+a_{x}\left(t-1\right)\gamma \quad {\text{ avec }}\quad v_{x}\left(0\right)=v_{i}\cos \left(\alpha \right)}$

${\displaystyle v_{y}\left(t\right)=v_{y}\left(t-1\right)+a_{y}\left(t-1\right)\gamma \quad {\text{ avec }}\quad v_{y}\left(0\right)=v_{i}\sin \left(\alpha \right)}$

${\displaystyle v\left(t\right)={\sqrt {v_{x}\left(t\right)^{2}+v_{y}\left(t\right)^{2}}}}$

${\displaystyle a_{x}\left(t\right)=-{\frac {1}{m}}k\ v\left(t\right)^{\lambda -1}\ v_{x}\left(t\right)}$

${\displaystyle a_{y}\left(t\right)=-g-{\frac {1}{m}}k\ v\left(t\right)^{\lambda -1}\ v_{y}\left(t\right)+{\frac {1}{m}}\rho \ V\ g}$

où λ désigne la puissance caractéristique de la résistance de fluide à laquelle est élevée la vitesse du projectile, et V le volume du projectile rempli du fluide.

Résolution analytique dans le cas quadratique

Lorsque la traînée est proportionnelle au carré de la vitesse du projectile, on fait face à un système d'équations différentielles non-linéaires couplées, et la résolution nécessite une approche plus engagée. Newton lui-même était incapable de résoudre le problème, mais son contemporain Johann Bernoulli réussit après avoir été mis au défi par l'astronome britannique John Keill^[2]. Sa solution est connue sous le nom d'équation de l'hodographe, et bien qu'elle soit la plus citée de la littérature physique, elle contient des termes qui ne peuvent être évalués que numériquement, c'est-à-dire que cette solution n'est pas une véritable solution analytique explicite.

Par véritable solution analytique, il faut comprendre une solution qui établisse les équations du mouvement pour toutes les conditions initiales, sans recourir à des approximations ou des simplifications qui ne sont valides que pour certains cas particuliers de conditions initiales. Une solution est explicite si elle dépend explicitement d'une variable indépendante naturelle, ici le temps, et non de plusieurs autres variables auxiliaires, comme le fait la solution de l'hodographe proposée par Johann Bernoulli.

Alors nous avons^[3]

${\displaystyle v_{x}\left(t\right)={\frac {v_{x_{0}}}{\phi \left(t\right)}}\quad {\text{ avec }}\quad v_{x_{0}}=v_{0}\cos \left(\alpha \right)}$

et

${\displaystyle v_{y}\left(t\right)={\frac {v_{y_{0}}-g\ \Phi \left(t\right)}{\phi \left(t\right)}}\quad {\text{ avec }}\quad v_{y_{0}}=v_{0}\sin \left(\alpha \right)}$

avec

${\displaystyle \phi (t)=\exp \left[\omega \ \int _{0}^{t}{\sqrt {v_{x}^{2}\left(s\right)+v_{y}^{2}\left(s\right)}}\ \mathrm {d} s\right]\quad {\text{ avec }}\quad \omega =-{\frac {k}{m}}}$

et

${\displaystyle \Phi ^{\prime }\left(t\right)=\phi \left(t\right)}$

de laquelle il existe un développement en série de Maclaurin qui s’écrit :

${\displaystyle \Phi \left(t\right)=\sum _{j=0}^{+\infty }{\frac {\Phi ^{(j)}(0)}{j!}}\ t^{j}\quad }$

avec ${\displaystyle \Phi (0)=0}$ et ${\displaystyle \Phi ^{\prime }(0)=1}$, et pour tout entier naturel j

${\displaystyle \Phi ^{(j+2)}\left(0\right)=\omega \ {\sqrt {v_{x_{0}}^{2}+\left(v_{y_{0}}-g\ \Phi ^{(j)}\left(0\right)\right)^{2}}}}$.

Détermination de la traînée

On rappelle que ${\displaystyle \mathrm {R_{e}} ={\frac {v\ L\ \rho }{\eta }}}$ avec v la vitesse relative du fluide en mètre par seconde, L la taille caractéristique de l’écoulement en mètre, ρ la masse volumique du fluide en kilogramme par mètre cube, et η la viscosité dynamique du fluide en pascal-seconde.

Lorsque ${\displaystyle \mathrm {R_{e}} <\!\!<1}$, l'écoulement suit une loi de Stokes. En particulier, dans le cas d'une sphère, la traînée F_T s'exprime

${\displaystyle F_{T}=-3\ \pi \ \eta \ D\ v\quad }$ avec η la viscosité dynamique du fluide, D le diamètre de la sphère, et v la vitesse du mobile.

Alors le coefficient de proportionnalité k s'écrit ${\displaystyle k=-3\pi \,\eta \,D}$.

Lorsque ${\displaystyle 30<\mathrm {R_{e}} <800}$, l'écoulement suit une loi de Poiseuille.

Lorsque ${\displaystyle \mathrm {R_{e}} >2000}$, l'écoulement est turbulent et la traînée F_T s'exprime

${\displaystyle F_{T}={\frac {1}{2}}\ \rho \ S\ C_{x}\ v^{2}\quad }$ avec S la surface de référence du projectile, C_x le coefficient de traînée du projectile.

Alors le coefficient de proportionnalité ${\displaystyle k}$ s'écrit ${\displaystyle k={\frac {1}{2}}\rho \,S\,C_{x}}$.

Taille caractéristique de l'écoulement

Pour l'étude de la traînée des corps géométriques, lorsque l'objet est profilé, la taille de caractéristique de l'écoulement est la largeur de sa surface frontale. Lorsque l'objet est non-profilé, il s'agit de la longueur de sa surface parallèle à l'écoulement.

Masse volumique

La masse volumique de l’air est fonction de la température, de la masse molaire et de la pression. En choisissant pour pression celle de l'atmosphère standard internationale (ISA) au niveau de la mer : P₀ = 101 325 Pa = 1 013,25 mbar = 1 013,25 hPa, on peut considérer que

${\displaystyle \rho _{\mathrm {air} }=1,292\times {\frac {273,15}{T}}\quad }$ avec T en kelvins.

Plus généralement, on peut se référer aux tables des masses volumiques de diverses substances.

Viscosité dynamique

On peut utiliser la loi semi-empirique de Sutherland pour déterminer la viscosité dynamique dans l'air^[4] :

${\displaystyle \eta _{\mathrm {air} }=B{\frac {\sqrt {T}}{1+{\frac {c}{T}}}}\quad }$ avec ${\displaystyle B=1,4810^{-6}\;\mathrm {Ns} \ \mathrm {K} ^{-0{,}5}\mathrm {m} ^{2}}$ et ${\displaystyle c=119,4\;\mathrm {K} }$ des constantes déterminées empiriquement, et T la température de l’air en kelvins.

Surface de référence

Lorsque l'objet est profilé, la surface de référence du mobile est sa surface frontale, c'est-à-dire la surface occupée par l'objet sur la projection perpendiculaire à l'écoulement. Lorsque l'objet est non-profilé, la surface de référence du mobile est sa surface alaire.

Coefficient de traînée

Le coefficient de traînée ${\displaystyle C_{x}}$ est un nombre sans dimension dont la valeur peut être déterminée expérimentalement en soufflerie.

Bien que le coefficient de traînée soit fonction du nombre de Reynolds, on peut tout de même utiliser en première approximation les coefficients de traînée de l'image ci-contre.

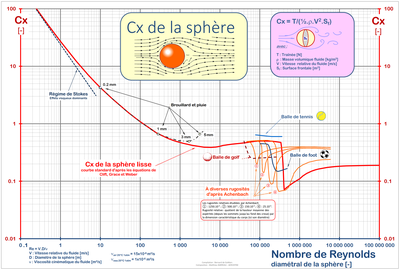
On peut aussi, dans le cas d'une sphère, se référer à ce graphique qui donne le coefficient de traînée en fonction du nombre de Reynolds. Dans certaines plages de ce nombre de Reynolds, les ingénieurs considèrent souvent le ${\displaystyle C_{x}}$ de la sphère comme constant.

Notes et références

Notes

Références

• Portail de la physique