Méthode d'Euler

En mathématiques, la méthode d'Euler, nommée ainsi en l'honneur du mathématicien Leonhard Euler (1707 — 1783), est une procédure numérique pour résoudre par approximation des équations différentielles du premier ordre avec une condition initiale. C'est la plus simple des méthodes de résolution numérique des équations différentielles.

Principe de la méthode

La méthode d'Euler est une méthode numérique élémentaire de résolution d'équations différentielles du premier ordre, de la forme

${\displaystyle \forall x\in I,u'(x)=f(x,u(x))}$

où I est un intervalle de ${\displaystyle \mathbb {R} }$ et f, une fonction réelle sur ${\displaystyle I\times \mathbb {R} }$.

Étant donné une condition initiale ${\displaystyle (a,u(a))\in I\times \mathbb {R} }$, la méthode fournit pour tout point b ∈ I une suite ${\displaystyle (u_{n}(b))_{n\in \mathbb {N} }}$ d'approximations de la valeur u(b) que prend, lorsqu'elle existe, la solution de l'équation qui correspond à cette condition initiale. Divers jeux de conditions sur f peuvent assurer la convergence de cette suite.

La valeur u_n(b) s'obtient en calculant n + 1 valeurs intermédiaires ${\displaystyle (y_{i})_{i=0}^{n}}$ de la solution approchée aux points ${\displaystyle (x_{i})_{i=0}^{n}}$ régulièrement répartis entre a et b, donnés par

${\displaystyle x_{i}=a+i{\frac {b-a}{n}}.}$

Euler explicite

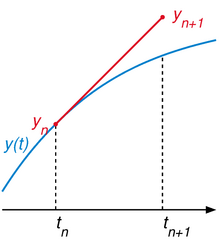
En étendant cette notation à x₀ = a, y₀ = u(a) et x_n = b, y_n = u_n(b) et en utilisant l'approximation de la dérivée

${\displaystyle u'(x_{i})\simeq {\frac {u(x_{i+1})-u(x_{i})}{x_{i+1}-x_{i}}}}$

On en déduit la relation suivante :

${\displaystyle {\frac {y_{i+1}-y_{i}}{x_{i+1}-x_{i}}}=f(x_{i},y_{i})}$

Les valeurs intermédiaires sont alors données par la relation de récurrence

${\displaystyle y_{i+1}=y_{i}+(x_{i+1}-x_{i})f(x_{i},y_{i}),\ i\in [\![0,n-1]\!].}$

qui est le schéma d'Euler explicite.

Euler implicite

En remarquant que l'on peut aussi approcher la dérivée en x_{i +1} par la même relation

${\displaystyle u'(x_{i+1})\approx {\frac {u(x_{i+1})-u(x_{i})}{x_{i+1}-x_{i}}}}$

on en déduit la relation de récurrence

${\displaystyle y_{i+1}=y_{i}+(x_{i+1}-x_{i})f(x_{i+1},y_{i+1}),\ i\in \ [\![0;n-1]\!]}$

qui est le schéma d'Euler implicite. On notera que dans ce schéma, le terme y_{i +1} apparaît des deux côtés de l'équation, ce qui contraint à utiliser des méthodes de résolution numérique du type de la méthode de Newton-Raphson pour déterminer y_{i +1} à chaque itération si la fonction f est non linéaire.

Exemples

Application à l'intégration

L'intégration d'une fonction continue sur un segment peut être vue comme un cas particulier où la fonction f est continue et ne dépend que de x : ${\displaystyle u'(x)=f(x)}$. On démontre alors, en utilisant la continuité uniforme de f sur [a ,b] (théorème de Heine), que la suite ${\displaystyle (u_{n}(b))_{n\in \mathbb {N} }}$ est de Cauchy, et donc converge par complétude de ${\displaystyle \mathbb {R} }$.

En fait, on a : ${\displaystyle y_{n}=h\sum _{k=0}^{n-1}f(a+kh)={\frac {b-a}{n}}\sum _{k=0}^{n-1}f\left(a+k{\frac {b-a}{n}}\right).}$

On reconnaît la méthode des rectangles à gauche pour le calcul de la solution exacte ${\displaystyle \int _{a}^{x_{n}}f(u)\,du}$.

Exemple

${\displaystyle f(x)={\frac {x}{2}}}$

Étant donné la fonction ${\displaystyle f:x\mapsto {\frac {x}{2}}}$ et les valeurs initiales x₀ = 1 et y₀ = F(x₀) = ¹⁄₄.

Le calcul des valeurs F(x₁), F(x₂), F(x₃)… permet d'obtenir la représentation graphique de F par les segments [A₀A₁], [A₁A₂], [A₂A₃]…

La fonction f a pour primitive ${\displaystyle G:x\mapsto {\frac {x^{2}}{4}}}$ avec x₀ = 1 et y₀ = G(x₀) = ¹⁄₄.

La courbe (C) représentative de G est ici placée sur le même graphe pour visualiser le calcul des tangentes.

La fonction affine par morceaux est une approximation de la primitive G.

Cas linéaire

Un autre cas classique est celui où f est une fonction linéaire en u : ${\displaystyle u'=cu}$. Le schéma donne alors :

${\displaystyle y_{n+1}=y_{n}+hcy_{n}=(1+ch)y_{n},}$ soit

${\displaystyle y_{n}=(1+ch)^{n}=\left(1+c{\frac {b-a}{N}}\right)^{n}.}$

On retrouve au point final une valeur approchée de la solution exacte pour peu que N soit suffisamment grand : ${\displaystyle y_{N}=\left(1+c{\frac {b-a}{N}}\right)^{N}\simeq \exp(c(b-a))}$.

On peut également constater que si le pas est trop grand, la suite (géométrique) prend des valeurs de plus en plus grandes et diverge de la solution (le schéma est instable). Un palliatif est d'utiliser une méthode d'Euler implicite : ${\displaystyle y_{n+1}=y_{n}+hcy_{n+1}\Longleftrightarrow y_{n}=(1-ch)^{-n}.}$

Ce schéma est plus stable numériquement et garantit plus simplement la convergence vers la solution.

Erreur de la méthode

La méthode d'Euler est simple mais l'erreur induite peut être assez élevée si le pas est choisi trop grand. En effet, le calcul de l'erreur de consistance donne par la formule de Taylor-Lagrange : ${\displaystyle \epsilon _{n}=u(t_{n+1})-u_{n+1}=u(t_{n+1})-u(t_{n})-hf(t_{n},u(t_{n}))=u(t_{n+1})-u(t_{n})-hu'(t_{n})={\frac {1}{2}}h^{2}u''(t_{n})+o(h^{2}).}$

Voir aussi

Articles connexes

• Méthodes de Runge-Kutta (utilisent le même principe que celle d'Euler mais apportent une meilleure précision)
• Méthode d'Euler semi-implicite
• Théorème de Cauchy-Peano-Arzelà
• Méthode Leapfrog

Liens externes

• Méthode d'Euler. Construction point par point d'une courbe intégrale avec GéoPlan. sur le site de P. Debart
• (en) Eric W. Weisstein, « Euler Backward Method », sur MathWorld
• (en) Eric W. Weisstein, « Euler Forward Method », sur MathWorld

• Portail de l'analyse