Droite d'Euler

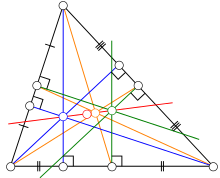
En géométrie euclidienne, dans un triangle non équilatéral, la droite d'Euler est une droite passant par plusieurs points remarquables du triangle, dont l'orthocentre, le centre de gravité (ou isobarycentre) et le centre du cercle circonscrit.

Cette notion s'étend au quadrilatère inscriptible et au tétraèdre.

Présentation

Euler établit en 1765 que dans un triangle non équilatéral (ABC), l'orthocentre H, le centre de gravité (ou isobarycentre) G et le centre du cercle circonscrit O sont alignés, et détermine les relations de proportionnalité entre les distances : HO = 3/2HG et GO = 1/2HG^[1]. La droite (HGO) passe également par le centre Ω du cercle des neuf points, milieu du segment [OH], ainsi que par d'autres points remarquables du triangle^[2]. Les quatre points H,G,O,Ω sont confondus pour un triangle équilatéral (et sinon, ils sont tous distincts).

Parmi les autres points remarquables, on peut citer le point de Longchamps, le point de Schiffler, le point d'Exeter et le perspecteur de Gossard.

En revanche, elle ne passe pas par le centre du cercle inscrit dans le triangle, sauf si celui-ci est isocèle. Dans ce cas, la droite d'Euler est l'axe de symétrie du triangle.

Détermination

Relation vectorielle d'Euler

La relation vectorielle d'Euler : ${\overrightarrow {OH}}=3{\overrightarrow {OG}}$ exprime à la fois l'alignement de $H,G,O$ et leur disposition mutuelle.

Démonstration de la relation d'Euler

Si l'on admet la relation de Sylvester qui s'écrit :

{\overrightarrow {OH}}={\overrightarrow {OA}}+{\overrightarrow {OB}}+{\overrightarrow {OC}}

la relation d'Euler s'en déduit directement puisque le centre de gravité ou isobarycentre du triangle vérifie $3{\overrightarrow {OG}}={\overrightarrow {OA}}+{\overrightarrow {OB}}+{\overrightarrow {OC}}$ .

On peut également démontrer l'égalité à l'aide de l'homothétie de centre G et de rapport -1/2. La position de G au deux tiers des médianes permet de dire que l'image de (ABC) par cette homothétie est le triangle $(I_{1},I_{2},I_{3})$ ayant pour sommets les milieux des côtés du triangle (ABC). Les images des hauteurs par cette homothétie sont des droites parallèles aux hauteurs et passant par $(I_{1},I_{2},I_{3})$ sont les médiatrices du triangle (ABC). L'image de H, point de concours des hauteurs, est alors O, le point de concours des médiatrices. Les points G, H et O sont donc bien alignés et on a : ${\overrightarrow {GO}}=-{\frac {1}{2}}{\overrightarrow {GH}}$ d'où ${\overrightarrow {OH}}=3{\overrightarrow {OG}}$

Représentations

Équation

On note ${\widehat {A}},{\widehat {B}},{\widehat {C}}$ les angles aux sommets du triangle de référence, et on considère un point M de coordonnées trilinéaires (x : y : z). L'équation de la droite d'Euler s'écrit alors

\sin(2{\hat {A}})\sin({\hat {B}}-{\hat {C}})x+\sin(2{\hat {B}})\sin({\hat {C}}-{\hat {A}})y+\sin(2{\hat {C}})\sin({\hat {A}}-{\hat {B}})z=0.

En coordonnées barycentriques $(\alpha ,\beta ,\gamma )$ , l'équation s'écrit ^[3]

(\tan {\hat {C}}-\tan {\hat {B}})\alpha +(\tan {\hat {A}}-\tan {\hat {C}})\beta +(\tan {\hat {B}}-\tan {\hat {A}})\gamma =0.

Représentation paramétrique

On sait que le centre du cercle circonscrit a pour coordonnées trilinéaires (cos A : cos B : cos C) et que celles de l'orthocentre sont ( cos B cos C : cos C cos A : cos A cos B). Ainsi, tout point de la droite d'Euler différent de l'orthocentre a pour coordonnées trilinéaires :

(\cos {\hat {A}}+t\cos {\hat {B}}\cos {\hat {C}}:\cos {\hat {B}}+t\cos {\hat {C}}\cos {\hat {A}}:\cos {\hat {C}}+t\cos {\hat {A}}\cos {\hat {B}})

avec t réel.

Ainsi, on obtient :

le centre du cercle circonscrit pour t = 0,
le centre de gravité, de coordonnées (cos A + cos B cos C : cos B + cos C cos A : cos C + cos A cos B), pour t = 1,
le centre du cercle d'Euler, de coordonnées (cos A + 2cos B cos C : cos B + 2cos C cos A : cos C + 2cos A cos B), pour t = 2,
le point de Longchamps, de coordonnées (cos A – cos B cos C : cos B – cos C cos A : cos C – cos A cos B), pour t = –1.

Longueurs des segments

Les longueurs des différents segments s'expriment en fonction des trois côtés du triangle et du rayon du cercle circonscrit : $OG^{2}=R^{2}-{\frac {1}{9}}(a^{2}+b^{2}+c^{2})$ et donc, d'après la relation d'Euler ci-dessus, $OH^{2}=9R^{2}-(a^{2}+b^{2}+c^{2})$

où $(a,b,c)=(BC,CA,AB)$ et $R$ est le rayon du cercle circonscrit à $(ABC)$ ^[4]^,^[5].

Comme de plus, $R^{2}={a^{2}b^{2}c^{2} \over {(a+b+c)(-a+b+c)(a-b+c)(a+b-c)}}$ , $OG,OH{\text{ et }}GH$ s'expriment comme fonctions symétriques des longueurs a, b et c.

Démonstration de l'égalité concernant OG

D'après la formule de la fonction scalaire de Leibnitz $f(M)=f(G)+3MG^{2}$ , on a :

OA^{2}+OB^{2}+OC^{2}=GA^{2}+GB^{2}+GC^{2}+3OG^{2}

On a donc :

OG^{2}=R^{2}-{\frac {1}{3}}(AG^{2}+BG^{2}+CG^{2}).

Considérons maintenant le point A', symétrique de A par rapport au milieu I₁ de [BC].

D'une part, ${\overrightarrow {AG}}={\frac {2}{3}}{\overrightarrow {AI_{1}}}={\frac {1}{3}}{\overrightarrow {AA'}}.$
D'autre part, (ABA'C) est un parallélogramme, et la règle du parallélogramme indique que :

AA'^{2}+a^{2}=2b^{2}+2c^{2}.

Donc $AG^{2}={\frac {1}{9}}AA'^{2}={\frac {1}{9}}(2b^{2}+2c^{2}-a^{2}),$

AG^{2}+BG^{2}+CG^{2}={\frac {1}{3}}(a^{2}+b^{2}+c^{2}),

et finalement :

OG^{2}=R^{2}-{\frac {1}{9}}(a^{2}+b^{2}+c^{2}).

Extension au tétraèdre

Le tétraèdre possède aussi une droite remarquable, désignée par analogie "droite d'Euler". Elle est définie pour un tétraèdre non équifacial par les trois points suivants :

le centre de gravité G, point d'intersection des quatre droites joignant un sommet au centre de gravité de la face opposée, ainsi que des trois droites joignant les milieux de deux arêtes opposées

le point de Monge M, intersection des six plans orthogonaux à une arête et passant par le milieu de l'arête opposée ^[6]

le centre de la sphère circonscrite O.

Le centre de gravité est le milieu du segment joignant centre de la sphère circonscrite au point de Monge $({\overrightarrow {OM}}=2{\overrightarrow {OG}})$ .

Il existe aussi une sphère des douze points, ou première sphère d'Euler, dont le centre $\Omega$ se trouve sur la droite d'Euler $({\overrightarrow {O\Omega }}={\frac {2}{3}}{\overrightarrow {OM}})$ .

Références

(en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Euler line » (voir la liste des auteurs).

↑ (la) Leonhard Euler, Solutio facilis problematum quorundam geometricorum difficillimorum (lire en ligne) sur le site de Euler Archive, rem page 114.
↑ (en) Eric W. Weisstein, « Euler Line », sur MathWorld
↑ (en) J.A. Scott, « Some examples of the use of areal coordinates in triangle geometry », Mathematical Gazette, n^o 83,‎ novembre 1999, p. 472-477.
↑ La preuve donnée ici est inspirée de celle donnée par Alexander Bogomolny sur la page Sum of Squares of Distances to Vertices de Cut The Knot.
↑ Une autre preuve, faisant appel aux nombres complexes, est proposée par Bogomolny sur la page Distance between the Orthocenter and Circumcenter
↑ Point de Monge d'un tétraèdre.

Voir aussi

Bibliographie

Jean-Denis Eiden, Géométrie analytique classique, Calvage et Mounet, 2009 (ISBN 978-2-91-635208-4)
Petite encyclopédie de mathématique, Didier
Jean Fresnel, Méthodes modernes en géométrie, Paris, Hermann, 2010, 3^e éd., 411 p. (ISBN 978-2-7056-7084-9)
Bruno Ingrao, Coniques affines, euclidiennes et projectives, Calvage et Mounet (ISBN 978-2-916352-12-1)

v · m Triangles
Description	Sommet Apex Côté Angle Base
Types	Triangle équilatéral Triangle isocèle Triangle d'or Triangle rectangle Angle droit Cathète Hypoténuse Triangle de Kepler Triangle obtusangle Triangle acutangle Triangle isocèle rectangle Triangle pseudo-rectangle Triangle scalène Triangle de Héron
Points remarquables (Nombre de Kimberling)	Centres : Centre du cercle inscrit Centre de gravité Centre du cercle circonscrit Orthocentre Centre du cercle d'Euler Centre du cercle de Spieker Points de Brocard Points de Feuerbach Point de Fermat ou Point de Torricelli Point de Longchamps Point de Miquel Point de Gergonne Point de Nagel Point de Vecten Points isogonaux Points isodynamiques Point de Lemoine Points de Terquem Points de Napoléon Mittenpunkt
Droites remarquables	Cévienne Hauteur Médiane Bissectrice Médiatrice Droite de Brocard Droite d'Euler Droite de Lemoine Droite de Newton Droite de Simson (ou droite de Wallace) Droite de Steiner Ménélienne Symédiane Axe orthique Droite centrale
Cercles remarquables	Cercle circonscrit Cercle exinscrit Cercle inscrit Cercle d'Euler Cercle d'Apollonius Cercles de Lemoine Cercle de Longchamps Cercle de Miquel Cercle de Taylor Cercle de Tucker Cercle podaire Cercle de Brocard Cercle de Spieker Cercle de Fuhrmann Cercles de Johnson Cercle pédal
Triangles remarquables	Triangle de Bevan Triangle de Feuerbach Triangle de Gergonne Triangle de Morley Triangle de Nagel Triangle inscrit de périmètre minimal (Problème de Fagnano) Triangle médian Triangle orthique Triangle podaire Triangle tangentiel Triangle de Fuhrmann
Courbes remarquables	Deltoïde de Steiner Coniques Conique inscrite de Serret (ou de MacBeath) Conique orthique Hyperbole de Kiepert Paraboles Parabole tritangente Parabole de Kiepert Ellipses Ellipse de Mandart Ellipse de Steiner Coniques circonscrites et inscrites à un triangle Cubiques
Théorèmes	Théorème de Pythagore Théorème de Thalès Théorème de Napoléon Théorème japonais de Carnot Théorème de Ménélaüs Théorème de Morley Théorème de Nagel Théorème de Neuberg Théorème de Hamilton Théorème d'Euler Théorème de Feuerbach Théorème de Viviani Avec des céviennes Théorème de Ceva Théorème de Gergonne Théorème de Stewart Théorème de Terquem Théorème de Routh Théorème de Jacobi Avec des cercles Théorème des six cercles Théorème des trois cercles de Miquel
Relations entre triangles	Triangles isométriques Triangles semblables Inégalités dans le triangle
Résolution	Loi des cosinus Loi des sinus Loi des tangentes Loi des cotangentes Aire Formule de Héron