Quádrica

Quádrica ou superfície quádrica é, em matemática, o conjunto dos pontos do espaço tridimensional cujas coordenadas formam um polinômio de segundo grau de no máximo três variáveis denominada de equação cartesiana da superfície:

  • A x 2 + B y 2 + C z 2 + D x y + E x z + F y z + G x + H y + I z + J = 0 {\displaystyle Ax^{2}+By^{2}+Cz^{2}+Dxy+Exz+Fyz+Gx+Hy+Iz+J=0\,} onde pelo menos um dos coeficientes a, b, c, d, e ou f é diferente zero, representando assim uma superfície quádrica, ou simplesmente, uma quádrica. Se a superfície quádrica, for cortada pelos planos coordenados ou por planos paralelos a eles, a curva de interseção será uma cônica. A interseção de uma superfície com um plano é chamado de traço da superfície no plano. A redução da equação geral das quádricas às suas formas mais simples exige cálculos laboriosos.

Plano cartesiano

Como a dimensão do plano é 2, ou R 2 {\displaystyle \mathbb {R} ^{2}} , as quádricas no plano cartesiano têm dimensão um e são curvas planas. Também são chamados de seções cónicas ou cónicas.

Círculo (e = 0), elipse (e = 0.5), parábola (e = 1) e hipérbole (e = 2) com um foco fixo F e uma diretriz.

Superfícies

Numa visão informal, as superfícies quadráticas são as regiões formadas quando as cônicas se movimentam no espaço. A partir da equação geral do segundo grau nas três variáveis x,y,z é possível representar uma superfície quadrática.

Observemos que se a superfície quadrática formada pela equação geral, for cortada por um plano paralelo a um dos planos coordenados, a curva de interseção será uma cônica.

Superfície Esférica

A superfície esférica S de centro C e raio r > 0 é o lugar geométrico dos pontos do espaço que mantém a distância r de C. Sendo P = ( x , y , z ) ∈ S {\displaystyle P=(x,y,z)\in S\,} e C = ( x o , y o , z o ) {\displaystyle (x_{o},y_{o},z_{o})\,} então d(P,C) = r, ou seja, a equação implícita de S é:

( x − x o ) 2 + ( y − y o ) 2 + ( z − z o ) 2 = r 2 {\displaystyle (x-x_{o})^{2}+(y-y_{o})^{2}+(z-z_{o})^{2}=r^{2}\,}

Se aproximarmos um plano π {\displaystyle \pi \,} de uma superfície esférica de modo que este toque a superfície em apenas um ponto Pt, este ponto é chamado ponto de tangência onde é válido:

π ∩ S = { P t } {\displaystyle \pi \cap S=\{Pt\}\,}

C   P t ¯ ⊥ π {\displaystyle {\overline {C\ Pt}}\perp \pi \,}

d ( C , π ) = r {\displaystyle d(C,\pi )=r\,}

Porém, se o plano π {\displaystyle \pi } tocar a superfície em mais de um ponto, então o plano é secante à superfície, o que acontece sempre que d ( C , π ) < r {\displaystyle d(C,\pi )<r\,} .

Superfície Cilíndrica

Uma superfície é dita cilíndrica se existir uma curva C e uma reta r tais que a superfície seja a união de retas paralelas a r que passem por C. C é chamada diretriz da superfície S e as retas paralelas a r são geratrizes de S.

Se a curva C for uma quádrica plana, então a superfície será uma quádrica no espaço.

Superfície Cônica

Uma superfície S é dita cônica se ela for formada a partir de uma curva C e um ponto V não pertencente a C tal que S é a união das retas VQ, onde Q percorre C.

Se a curva C for uma quádrica plana, então a superfície será uma quádrica no espaço.

Superfície de Rotação

Uma superfície S é uma superfície de rotação se existem uma reta r e uma curva C tal que S é a união das circunferências com centro em r e que tangenciam C.

r é o eixo de rotação de S. A interseção de S com o semiplano de origem r é um meridiano de S.

Na maioria dos casos em que a curva C é uma quádrica plana, a superfície tem grau maior que 2 (não sendo uma quádrica; por exemplo, se C for um círculo que não intercepta r, S será um toro).

S será uma quádrica quando C, além de ser uma quádrica, ainda tem r como eixo de simetria.

Superfícies Quádricas

Relação das superfícies quádricas da sua fórmula e desenho:
Superfície quádrica Fórmulas Desenho
Elipsoide x 2 a 2 + y 2 b 2 + z 2 c 2 = 1 {\displaystyle {x^{2} \over a^{2}}+{y^{2} \over b^{2}}+{z^{2} \over c^{2}}=1\,}
Elipsoide de revolução (caso particular do elipsoide) x 2 a 2 + y 2 a 2 + z 2 b 2 = 1 {\displaystyle {x^{2} \over a^{2}}+{y^{2} \over a^{2}}+{z^{2} \over b^{2}}=1\,}
Esfera (caso particular do elipsoide de revolução) x 2 a 2 + y 2 a 2 + z 2 a 2 = 1 {\displaystyle {x^{2} \over a^{2}}+{y^{2} \over a^{2}}+{z^{2} \over a^{2}}=1\,}
Paraboloide elíptico x 2 a 2 + y 2 b 2 − z = 0 {\displaystyle {x^{2} \over a^{2}}+{y^{2} \over b^{2}}-z=0\,}
Paraboloide de revolução (caso particular do paraboloide elíptico) x 2 a 2 + y 2 a 2 − z = 0 {\displaystyle {x^{2} \over a^{2}}+{y^{2} \over a^{2}}-z=0\,}
Paraboloide hiperbólico x 2 a 2 − y 2 b 2 − z = 0 {\displaystyle {x^{2} \over a^{2}}-{y^{2} \over b^{2}}-z=0\,}
Hiperboloide de uma folha 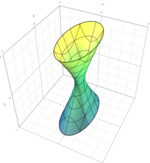x 2 a 2 + y 2 b 2 − z 2 c 2 = 1 {\displaystyle {x^{2} \over a^{2}}+{y^{2} \over b^{2}}-{z^{2} \over c^{2}}=1\,}
Hiperboloide de duas folhas 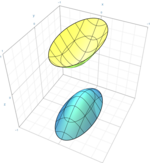− x 2 a 2 − y 2 b 2 + z 2 c 2 = 1 {\displaystyle -{x^{2} \over a^{2}}-{y^{2} \over b^{2}}+{z^{2} \over c^{2}}=1\,}
Cone x 2 a 2 + y 2 b 2 − z 2 c 2 = 0 {\displaystyle {x^{2} \over a^{2}}+{y^{2} \over b^{2}}-{z^{2} \over c^{2}}=0\,}
Cilindro elíptico x 2 a 2 + y 2 b 2 = 1 {\displaystyle {x^{2} \over a^{2}}+{y^{2} \over b^{2}}=1\,}
Cilindro circular (caso particular do Cilindro elíptico) x 2 a 2 + y 2 a 2 = 1 {\displaystyle {x^{2} \over a^{2}}+{y^{2} \over a^{2}}=1\,}
Cilindro hiperbólico x 2 a 2 − y 2 b 2 = 1 {\displaystyle {x^{2} \over a^{2}}-{y^{2} \over b^{2}}=1\,}
Cilindro parabólico x 2 + 2 y = 0 {\displaystyle x^{2}+2y=0\,}

Referências

Referências

  • Camargo, Ivan de; Boulos, Paulo. (2005). Geometria Analítica: um Tratamento Vetorial. Makron Books. 3ª edição. ISBN 8587918915.

Ligações externas

  • Applet interativo 3D em Java de todas as quádricas
  • Venturi, Jacir J. (2003). Cônicas e Quádricas (PDF). Curitiba: Unificado. 246 páginas. ISBN 85-85132-48-5