Norma (matemática)

Uma circunferência centrada na origem de R 2 {\displaystyle \mathbb {R} ^{2}} relativa a três normas distintas

Em matemática, uma norma consiste em uma função que a cada vetor de um espaço vetorial associa um número real não-negativo. O conceito de norma está intuitivamente relacionado à noção geométrica de comprimento.

Definição

Dado um espaço vetorial X {\displaystyle X} sobre o corpo K {\displaystyle \mathbb {K} } dos números reais ou complexos, uma função ‖ ⋅ ‖ : X → R + {\displaystyle \|\cdot \|:X\to \mathbb {R} ^{+}} é chamada de norma se, para quaisquer x , y ∈ X {\displaystyle x,y\in X} e todo α ∈ K : {\displaystyle \alpha \in \mathbb {K} :} [1]

  • ‖ x ‖ = 0 ⇔ x = 0 X . {\displaystyle \|x\|=0\Leftrightarrow x=0_{_{X}}.} Se esta condição não for atendida, a função será no máximo uma seminorma.
  • ‖ α x ‖ = | α | ‖ x ‖ {\displaystyle \|\alpha x\|=|\alpha |\|x\|}
  • ‖ x + y ‖ ⩽ ‖ x ‖ + ‖ y ‖ {\displaystyle \|x+y\|\leqslant \|x\|+\|y\|} (desigualdade triangular)

Se o espaço vetorial X {\displaystyle X} tem uma norma, ele passa a ser chamado de espaço normado, e denotado por ( X , ‖ ⋅ ‖ ) . {\displaystyle \left(X,\|\cdot \|\right).}

Métrica e topologia induzida

Toda norma induz de forma natural uma métrica d {\displaystyle d} em X {\displaystyle X} cujos valores são dados por:[2] d ( x , y ) = ‖ x − y ‖ . {\displaystyle d(x,y)=\|x-y\|\,.}

Também induz uma topologia localmente convexa que é gerada por todas as bolas:

B ( x 0 , r ) = { x ∈ X : d ( x , x 0 ) < r } ,     ∀ x ∈ X , ∀ r ∈ R + {\displaystyle B(x_{0},r)=\{x\in X:d(x,x_{0})<r\},~~\forall \,x\in X,\forall \,r\in \mathbb {R_{+}} }

Normas equivalentes

Duas normas ‖ ⋅ ‖ 1 {\displaystyle \|\cdot \|_{1}} e ‖ ⋅ ‖ 2 {\displaystyle \|\cdot \|_{2}} sobre o mesmo espaço vetorial X {\displaystyle X} são ditas equivalentes se existirem constantes reais positivas C 1 {\displaystyle C_{1}} e C 2 ( C 1 ⩽ C 2 ) {\displaystyle C_{2}\,(C_{1}\leqslant C_{2})} tais que: C 1 ‖ x ‖ 1 ⩽ ‖ x ‖ 2 ⩽ C 2 ‖ x ‖ 1     ∀ x ∈ X {\displaystyle C_{1}\|x\|_{1}\leqslant \|x\|_{2}\leqslant C_{2}\|x\|_{1}~~\forall \,x\in X}

Quando duas normas são equivalentes, elas induzem a mesma topologia.

Normas em espaços de dimensão finita

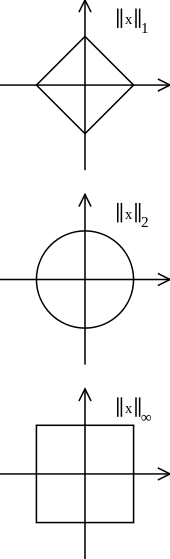
Seja x = ( x 1 , x 2 , … , x n ) = ∑ i = 1 n x i e i {\displaystyle x=\left(x_{1},x_{2},\ldots ,x_{n}\right)=\sum _{i=1}^{n}x_{i}e_{i}} a representação de um vetor em R n {\displaystyle \mathbb {R} ^{n}} ou C n . {\displaystyle \mathbb {C} ^{n}.}

As normas canônicas definidas nestes espaços são as chamadas normas ℓ p {\displaystyle \ell ^{p}} :

  • ‖ x ‖ p = ( ∑ i = 1 n | x i | p ) 1 p     , 1 ⩽ p < ∞ {\displaystyle \|x\|_{p}={\Big (}\sum _{i=1}^{n}|x_{i}|^{p}{\Big )}^{\frac {1}{p}}~~,1\leqslant p<\infty }
  • ‖ x ‖ ∞ = max i ∈ { 1 , … , n } | x i | {\displaystyle \|x\|_{\infty }=\max _{i\in \{1,\ldots ,n\}}|x_{i}|}

O caso particular em que p = 2 {\displaystyle p=2} corresponde à norma euclidiana: ‖ x ‖ 2 = ( ∑ i = 1 n | x i | 2 ) 1 2 {\displaystyle \|x\|_{2}={\Big (}\sum _{i=1}^{n}|x_{i}|^{2}{\Big )}^{\frac {1}{2}}}

Outras normas podem ainda ser definidas, no entanto, pode-se demonstrar que todas elas serão equivalentes.

Norma matricial

Ver artigo principal: Norma matricial

Se o espaço vetorial considerado é aquele formado pelas matrizes reais ou complexas de ordem n × m , {\displaystyle n\times m,} denotado por M n × m , {\displaystyle M^{n\times m},} uma norma sobre esse espaço é chamada de norma matricial. Um exemplo de norma matricial é a norma 1, denotada ‖ . ‖ 1 {\displaystyle \|.\|_{1}} definida como o máximo da soma módulo das entradas de cada linha, ou seja se A = [ a i j ] r × s {\displaystyle A=\left[a_{ij}\right]_{r\times s}} então a norma 1 da matriz A {\displaystyle A} é o número não negativo dado por[3] ‖ A ‖ 1 = max i ⩽ r ∑ j = 1 s | a i j | . {\displaystyle \|A\|_{1}=\max _{i\leqslant r}\sum _{j=1}^{s}|a_{ij}|.}

A norma 1 da matriz A = | 1 3 2 − 1 | , {\displaystyle A={\begin{vmatrix}1&3\\2&-1\end{vmatrix}},} por exemplo, é[4] ‖ A ‖ 1 = max { | 1 | + | 3 | , | 2 | + | − 1 | } = max { 4 , 3 } = 4. {\displaystyle \|A\|_{1}=\max \left\{|1|+|3|,|2|+|-1|\right\}=\max \left\{4,3\right\}=4.}

Normas em espaços de dimensão infinita

Espaços LP

Ver artigo principal: Espaço Lp

As normas ℓ p {\displaystyle \ell ^{p}} têm análogos em alguns espaços de dimensão infinita.

Produto interno

Ver artigo principal: Produto interno

Se um espaço vetorial possui um produto interno, este pode definir uma norma, dada pelo produto interno do vetor com ele mesmo.[5] ‖ v ‖ := ⟨ v , v ⟩ {\displaystyle \left\|v\right\|:={\sqrt {\langle v,v\rangle }}}

Se uma norma provém de um produto interno, ela satisfaz a identidade do paralelogramo.[6]

Notas

  1. ↑ SANTOS (2010), p.3, ex. 54.
  2. ↑ SANTOS (2010), p.60.
  3. ↑ Golub, Gene; Van Loan, Charles F. Matrix Computations 3 ed. Baltimore: The Johns Hopkins University Press. p. 56. ISBN 080185413X  A referência emprega parâmetros obsoletos |coautores= (ajuda)
  4. ↑ Boldrini et. al, p. 342.
  5. ↑ Lima 1981, p. 4.
  6. ↑ Lima 1981, p. 6.

Referências

  • SANTOS, José Carlos. Introdução à Topologia. Departamento de Matemática - Faculdade de Ciências da Universidade do Porto. Junho de 2010, 171 páginas. Disponível em: <http://www.fc.up.pt/mp/jcsantos/PDF/Topologia.pdf>. Acesso em: 12 jan. 2010. Página 60.
  • Boldrini, José Luiz et. al. Álgebra Linear 3ª ed. [S.l.]: Harbra. p. 342 
  • Lima, Elon Lages (1981). Curso de análise, Volume 2. Instituto de Matemática Pura e Aplicada. Rio de Janeiro: Instituto de Matemática Pura e Aplicada 

Ver também