Autômato com pilha

Na teoria dos autômatos, um autômato com pilha é um autômato finito com uma memória auxiliar em forma de pilha.

Operação

Autômatos com pilha diferem da definição normal de máquinas de estados finitos de duas maneiras:

1. Eles podem fazer uso da informação que está no topo da pilha para decidir qual transição deve ser efetuada;
2. Eles podem manipular a pilha ao efetuar uma transição.

Autômatos com pilha escolhem uma transição analisando o símbolo atual na cadeia de entrada, o estado atual e o topo da pilha. Máquinas de estados finitos convencionais apenas analisam o símbolo na cadeia de entrada e o estado atual. Autômatos com pilha adicionam a pilha como recurso auxiliar, deste modo, dado um símbolo da cadeia de entrada, o estado atual e um símbolo no topo da pilha, uma transição é selecionada.

Máquinas de estados finitos apenas escolhem um novo estado como resultado da sua transição, já os autômatos com pilha também podem manipular a pilha, como resultado de sua transição. A manipulação é feita através do desempilhamento de um símbolo da pilha ou através do empilhamento de um novo símbolo ao topo da mesma. Alternativamente, um autômato com pilha pode ignorar a pilha e deixá-la como está.

Os autômatos com pilha compreendem a classe das linguagens livres de contexto, de acordo com a Hierarquia de Chomsky e, portanto, são modelos de computação equivalentes às gramáticas livres de contexto.

Um autômato finito com acesso a duas pilhas possui capacidade de computação equivalente ao de uma máquina de Turing.^{[carece de fontes?]}

Definição formal

Um autômato de pilha é formalmente definido por uma 6-tupla:

${\displaystyle M=(Q,\ \Sigma ,\ \Gamma ,\ \Delta ,\ q_{0},\ F)}$

Onde:

• ${\displaystyle \,Q}$ é um conjunto finito de estados.
• ${\displaystyle \,\Sigma }$ é um conjunto finito de símbolos, denominado alfabeto de entrada.
• ${\displaystyle \,\Gamma }$ é um conjunto finito de símbolos, denominado alfabeto da pilha.
• ${\displaystyle \,\Delta \subseteq (Q\times \Sigma ^{*}\times \Gamma ^{*})\times (Q\times \Gamma ^{*})}$ é a relação de transição.
• ${\displaystyle \,q_{0}\in \,Q}$ é o estado inicial.
• ${\displaystyle F\subseteq Q}$ é o conjunto de estados finais (ou de aceitação).

Um elemento (p,a,α,q,β) é uma transição de M. Ela significa que M, estando no estado p, com o símbolo a na cadeia de entrada e com o símbolo α no topo da pilha, pode consumir o símbolo a, transitar para o estado q e desempilhar α substituindo-o por β. O ∑* e o Γ* denotam o fecho de Kleene do alfabeto de entrada e da pilha, respectivamente. Portanto, estes componentes são utilizados para formalizar que o autômato de pilha pode consumir qualquer quantidade de símbolos da cadeia de entrada e da pilha.

Computações

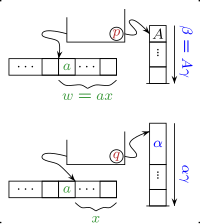
A fim de formalizar a descrição semântica dos autômatos com pilha, introduziremos uma descrição da situação atual. Qualquer 3-upla ${\displaystyle (p,w,\beta )\in Q\times \Sigma ^{*}\times \Gamma ^{*}}$ é chamada de uma descrição instantânea (ID) de ${\displaystyle M}$, que inclui o estado atual, a parte da cadeia de entrada que ainda não foi lida e o conteúdo da memória (o cabeçalho é escrito primeiro). A função de transição ${\displaystyle \delta }$ define a relação origina ${\displaystyle \vdash _{M}}$ de ${\displaystyle M}$ na descrição instantânea (ID). Para instruções ${\displaystyle (p,a,A,q,\alpha )\in \delta }$ existe um passo ${\displaystyle (p,ax,A\gamma )\vdash _{M}(q,x,\alpha \gamma )}$, para todo ${\displaystyle x\in \Sigma ^{*}}$ e todo ${\displaystyle \gamma \in \Gamma ^{*}}$.

Em geral, autômatos com pilha são não determinísticos, o que significa dizer que dada uma descrição instantânea ${\displaystyle (p,w,\beta )}$ pode haver diversos passos possíveis. Qualquer um desses passos pode ser escolhido durante uma computação. Com a definição acima, em cada passo um símbolo único (localizado no topo da pilha) é retirado e substituído por quantos símbolos forem necessários. Como consequência, nenhum passo é definido quando a pilha está vazia.

Computações dos autômatos com pilha são sequências de passos. A computação começa no estado inicial ${\displaystyle q_{0}}$com o símbolo inicial da pilha ${\displaystyle Z}$ na pilha e uma cadeia ${\displaystyle w}$ na fita de entrada e, portanto, com a descrição inicial ${\displaystyle (q_{0},w,Z)}$. Há duas maneiras de aceitar: O autômato com pilha aceita tanto por estado final, o que significa que depois de ler sua entrada, o autômato atinge um estado de aceitação (in ${\displaystyle F}$), quanto por pilha vazia (${\displaystyle \varepsilon }$), o que significa que após ler a cadeia de entrada, o autômato esvazia sua pilha. O primeiro modo de aceitação usa a memória interna, os estados, e o segundo modo a memória externa, a pilha.

Definição formal:

1. ${\displaystyle L(M)=\{w\in \Sigma ^{*}|(q_{0},w,Z)\vdash _{M}^{*}(f,\varepsilon ,\gamma )}$ com ${\displaystyle f\in F}$ e ${\displaystyle \gamma \in \Gamma ^{*}\}}$ (Estado final)
2. ${\displaystyle N(M)=\{w\in \Sigma ^{*}|(q_{0},w,Z)\vdash _{M}^{*}(q,\varepsilon ,\varepsilon )}$ com ${\displaystyle q\in Q\}}$ (Pilha vazia)

Aqui ${\displaystyle \vdash _{M}^{*}}$ representa os fechos reflexivos e transitivos da relação origina${\displaystyle \vdash _{M}}$ significando qualquer número de passos consecutivos (zero, um ou mais).

Para cada único autômato com pilha, essas duas linguagens não devem ter relação: eles podem ser iguais, mas normalmente não é o caso. Uma especificação do autômato deve também incluir o modo de aceitação pretendido. Entretanto, todos as condições de aceitação de um autômato com pilha definem uma mesma família de linguagem

Teorema Para todo autômato com pilha ${\displaystyle M}$ é possível construir um outro autômato com pilha ${\displaystyle M'}$ tal que ${\displaystyle L(M)=N(M')}$, e vice versa, para cada autômato com pilha ${\displaystyle M}$ é possível construir um autômato com pilha ${\displaystyle M'}$ tal que ${\displaystyle N(M)=L(M')}$

Exemplo

A seguir é a descrição formal do AP, que reconhece a linguagem ${\displaystyle \{0^{n}1^{n}\mid n\geq 0\}}$ por estado final:

${\displaystyle M=(Q,\ \Sigma ,\ \Gamma ,\ \delta ,\ p,\ Z,\ F)}$, onde

${\displaystyle Q=\{p,q,r\}}$

${\displaystyle \Sigma =\{0,1\}}$

${\displaystyle \Gamma =\{A,Z\}}$

${\displaystyle F=\{r\}}$

${\displaystyle \delta }$ consiste nas seis instruções seguintes:

${\displaystyle (p,0,Z,p,AZ)}$, ${\displaystyle (p,0,A,p,AA)}$, ${\displaystyle (p,\epsilon ,Z,q,Z)}$, ${\displaystyle (p,\epsilon ,A,q,A)}$, ${\displaystyle (q,1,A,q,\epsilon )}$, e ${\displaystyle (q,\epsilon ,Z,r,Z)}$.

Ou seja, no estado ${\displaystyle p}$ para cada símbolo ${\displaystyle 0}$ que for lido, um ${\displaystyle A}$ é colocado na pilha. Empilhar um símbolo ${\displaystyle A}$ no topo de um outro ${\displaystyle A}$ é formalizado como trocar o símbolo ${\displaystyle A}$ por ${\displaystyle AA}$. No estado ${\displaystyle q}$, para cada símbolo ${\displaystyle 1}$ lido, um ${\displaystyle A}$ a é desempilhado. Em um outro momento, o autômato se move do estado ${\displaystyle p}$ para o estado ${\displaystyle q}$, enquanto ele pode mover do estado ${\displaystyle q}$ para o estado de aceitação ${\displaystyle r}$ somente quando a pilha possuir um único ${\displaystyle Z}$.

Representamos a instrução ${\displaystyle (p,a,A,q,\alpha )}$ como uma ponte que sai do estado ${\displaystyle p}$ para o estado ${\displaystyle q}$ rotulada por ${\displaystyle a;A/\alpha }$ (leia ${\displaystyle a}$; substitui ${\displaystyle A}$ por ${\displaystyle \alpha }$).

Entendendo o processo de computação

A seguir ilustramos como o AP acima computa sobre diferentes cadeias de entrada.

(a) Cadeia de entrada = 0011. Há várias computações, dependendo do momento em que é feita a mudança do estado ${\displaystyle p}$ para o estado ${\displaystyle q}$. Apenas uma dessas computações aceita.

(i) ${\displaystyle (p,0011,Z)\vdash (q,0011,Z)\vdash (r,0011,Z)}$. O estado final é o de aceitação, mas a entrada não é aceita pois a cadeia não terminou de ser lida completamente.

(ii) ${\displaystyle (p,0011,Z)\vdash (p,011,AZ)\vdash (q,011,AZ)}$. Não há mais estados possíveis..

(iii) ${\displaystyle (p,0011,Z)\vdash (p,011,AZ)\vdash (p,11,AAZ)\vdash (q,11,AAZ)}$ ${\displaystyle \vdash (q,1,AZ)\vdash (q,\epsilon ,Z)}$ ${\displaystyle \vdash (r,\epsilon ,Z)}$. Computação de aceitação: termina em um estado de aceitação e a cadeia de entrada é lida totalmente.

(b) Cadeia de entrada = 00111. Novamente, há várias computações, mas nenhuma delas é uma computação de aceitação.

(i) ${\displaystyle (p,00111,Z)\vdash (q,00111,Z)\vdash (r,00111,Z)}$. O estado final é o de aceitação, mas a entrada não é aceita já que não foi lida.

(ii) ${\displaystyle (p,00111,Z)\vdash (p,0111,AZ)\vdash (q,0111,AZ)}$. Não há mais estados possíveis.

(iii) ${\displaystyle (p,00111,Z)\vdash (p,0111,AZ)\vdash (p,111,AAZ)\vdash (q,111,AAZ)}$ ${\displaystyle \vdash (q,11,AZ)\vdash (q,1,Z)}$ ${\displaystyle \vdash (r,1,Z)}$. O estado final é o de aceitação, mas a entrada não é aceita pois a cadeia não terminou de ser lida completamente.

AP e Linguagens livres de contexto

Toda gramática livre de contexto pode ser transformada em um autômato com pilha equivalente. O processo de derivação da gramática é simulada de uma forma mais à esquerda. Onde a gramática reescreve um não-terminal, o AP toma o não-terminal do topo da pilha pilha e substitui-la pelo lado direito de uma regra gramatical. Onde a gramática gera um símbolo terminal, o PDA lê um símbolo de entrada quando é o símbolo mais alto na pilha. De certa forma, a pilha do PDA contém os dados não transformados da gramática, correspondente a um percurso pré-ordem de uma árvore de derivação.

Tecnicamente, dada uma gramática livre de contexto, o AP é construído da seguinte forma:

1. ${\displaystyle (1,\varepsilon ,A,1,\alpha )}$ para cada regra ${\displaystyle A\to \alpha }$ (expand)
2. ${\displaystyle (1,a,a,1,\varepsilon )}$ para cada símbolo de terminal ${\displaystyle a}$ (match)

Como resultado, obtemos um autômato com pilha de um único estado. O estado aqui é ${\displaystyle 1}$, aceitando a linguagem livre de contexto por pilha vazia. O símbolo inicial da pilha é igual ao axioma da gramática livre do contexto.

O inverso, encontrar uma gramática para um AP dado, não é tão simples. O truque é codificar dois estados do AP em símbolos não-terminais da gramática.

Teorema Para cada autômato com pilha ${\displaystyle M}$ é possível construir uma gramática livre do contexto ${\displaystyle G}$ tal que ${\displaystyle N(M)=L(G)}$.

Autômato com Pilha Generalizado

Um Autômato com Pilha Generalizado APG é um AP que escreve uma cadeia inteira de um tamanho qualquer conhecido na pilha ou remove uma cadeia inteira da pilha em um único passo.

Um APG é formalmente definido como uma 6-upla:

${\displaystyle M=(Q,\ \Sigma ,\ \Gamma ,\ \delta ,\ q_{0},\ F)}$

onde Q, ${\displaystyle \Sigma \,}$, ${\displaystyle \Gamma \,}$, q₀ e F são definidos da mesma forma que um AP.

${\displaystyle \,\delta }$: ${\displaystyle Q\times \Sigma _{\epsilon }\times \Gamma ^{*}\longrightarrow P(Q\times \Gamma ^{*})}$

é a função de transição.

Regras de computação para um APG são as mesmas que para AP, exceto que a_i+1's e b_i+1's são agora cadeias ao invés de símbolos.

APGs e APs são equivalentes, ou seja, se uma linguagem é reconhecida por um AP, ela também é reconhecida por um APG, e vice-versa.

Podemos formular uma prova analítica da equivalência entre APGs e APs usando a seguinte simulação:

Faça ${\displaystyle \delta }$(q₁, w, x₁x₂...x_m) ${\displaystyle \longrightarrow }$ (q₂, y₁y₂...y_n) ser uma transição do APG

Onde ${\displaystyle q_{1},q_{2}\in Q}$, ${\displaystyle w\in \Sigma _{\epsilon }}$, ${\displaystyle x_{1},x_{2},\ldots ,x_{m}\in \Gamma ^{*}}$, ${\displaystyle m\geq 0}$, ${\displaystyle y_{1},y_{2},\ldots ,y_{n}\in \Gamma ^{*}}$, ${\displaystyle n\geq 0}$.

Construa as seguintes transições para o AP:

${\displaystyle \delta ^{'}}$(q₁, w, x₁) ${\displaystyle \longrightarrow }$ (p₁, ${\displaystyle \epsilon }$)

${\displaystyle \delta ^{'}}$(p₁, ${\displaystyle \epsilon }$, x₂) ${\displaystyle \longrightarrow }$ (p₂, ${\displaystyle \epsilon }$)

${\displaystyle \vdots }$

${\displaystyle \delta ^{'}}$(p_m-1, ${\displaystyle \epsilon }$, x_m) ${\displaystyle \longrightarrow }$ (p_m, ${\displaystyle \epsilon }$)

${\displaystyle \delta ^{'}}$(p_m, ${\displaystyle \epsilon }$, ${\displaystyle \epsilon }$ ) ${\displaystyle \longrightarrow }$ (p_m+1, y_n)

${\displaystyle \delta ^{'}}$(p_m+1, ${\displaystyle \epsilon }$, ${\displaystyle \epsilon }$ ) ${\displaystyle \longrightarrow }$ (p_m+2, y_n-1)

${\displaystyle \vdots }$

${\displaystyle \delta ^{'}}$(p_m+n-1, ${\displaystyle \epsilon }$, ${\displaystyle \epsilon }$ ) ${\displaystyle \longrightarrow }$ (q₂, y₁)

Softwares

• SCTMF- Software para Criação e Teste de Modelos Formais.
• JFlap- Software americano para testes com interface gráfica.

Teoria da computação

Teoria de autômatos: linguagem formal e gramática formal
Hierarquia Chomsky	Gramática	Linguagem	Reconhecedor
Tipo-0	Irrestrita	Recursivamente enumerável	Máquina de Turing
--	--	Recursiva	Máquina de Turing que sempre para
Tipo-1	Sensível ao contexto	Sensível ao contexto	Autômato linearmente limitado
Tipo-2	Livre de contexto	Livre de contexto	Autômato com pilha
Tipo-3	Regular	Regular	Autômato finito

Referências