ヒュッケル法(ヒュッケルほう、英: Hückel method)は、ドイツのエーリヒ・ヒュッケルによって提案された分子軌道法である。エチレンや1,3-ブタジエン、ベンゼン等のπ電子共役分子に適用する例が入門用としてよく用いられる。
ヒュッケル法では電子に関する積分に対して以下のような近似を導入する。
- 重なり積分の値は同じ原子軌道同士では1、異なる原子軌道の間では0
- クーロン積分(ハミルトニアン行列の対角要素)の値は同じ種類の原子では等しいものとし、パラメータ
 によって表す
によって表す - 共鳴積分(ハミルトニアン行列の非対角要素)の間に結合を持つ原子間でのみ0でない値をもつとし、パラメータ
 によって表す。
によって表す。
しばしば紹介されるπ共役系に対する計算では、その大胆な仮定にもかかわらず定性的に正しい結果を与え成功をおさめた。しかしながら結合を持つ原子間と持たない原子間とで積分の扱いを変えるため、構造を特定できていない分子に対しては適用できない。その欠点を改善するために、導入する近似を少なくし計算する積分の量を少し増やした拡張ヒュッケル法と呼ばれる方法があり、そちらと対比して単純ヒュッケル法とも呼ぶ。現在では計算機の性能の向上などにより単純ヒュッケル法を用いる必要性はほとんどなく、ただヒュッケル法、と言った場合には拡張ヒュッケル法を指すことが多い。
ヒュッケル法の仮定

重なり積分の値  は同じ原子軌道同士では1であり、異なる原子軌道間では0である。
は同じ原子軌道同士では1であり、異なる原子軌道間では0である。

 をクーロン積分と呼び、
をクーロン積分と呼び、 を共鳴積分と呼ぶ。結合を持たない原子間では
を共鳴積分と呼ぶ。結合を持たない原子間では の値は0。
の値は0。
1,3-ブタジエンの例
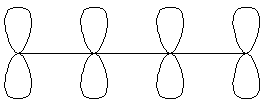
1,3-ブタジエンの分子軌道  を4つのπ軌道の線形結合で表す。
を4つのπ軌道の線形結合で表す。 は各π軌道の分子軌道への寄与の大きさである。
は各π軌道の分子軌道への寄与の大きさである。

変分法によってエネルギー を求めると、
を求めると、

この右辺を極小にする を定めることになる。実際に
を定めることになる。実際に を代入すると、
を代入すると、

と表せる。これを極小とするような を得る条件は、
を得る条件は、


である。これらの式が 以外の解を持つには、
以外の解を持つには、

である必要がある。これを永年方程式と呼ぶ。 ヒュッケル法の仮定より、

であるから、左辺を展開して、


 と置くと、行列式は
と置くと、行列式は

となり、その根は である。したがって、ブタジエンの4個の分子軌道のエネルギーは、
である。したがって、ブタジエンの4個の分子軌道のエネルギーは、

である。