コムフィルタ(英: comb filter)は、信号にそれ自身を遅延させたものを追加することで干渉を生じさせるフィルタ回路の一種である。くし形フィルタまたはくし型フィルタとも。コムフィルタの周波数特性は一定間隔のスパイク状になり、図示すると櫛のように見える。
用途
コムフィルタは様々な信号処理に利用されている。
技術的解説
コムフィルタにはフィードフォワード型とフィードバック型がある。これらの名称は追加する信号を遅延させる方向に対応している。
コムフィルタは、離散信号でも連続信号でも実装できる。ここでは主に離散信号での実装を解説する。連続信号用コムフィルタも特性はよく似ている。
フィードフォワード型
 フィードフォワード型コムフィルタの構造
フィードフォワード型コムフィルタの構造 フィードフォワード型コムフィルタの大まかな構造を右図に示す。これは次の式で表せる。
![{\displaystyle \ y[n]=x[n]+\alpha x[n-K]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d27304c28b441814595ccb92181af91876bb8b0c)
ここで、 は遅延長(標本数)、
は遅延長(標本数)、 は遅延信号に適用する倍率である。この式の両辺のZ変換を行うと、次の式が得られる。
は遅延信号に適用する倍率である。この式の両辺のZ変換を行うと、次の式が得られる。

伝達関数は次のように定義される。

周波数応答
 フィードフォワード型で
フィードフォワード型で  を様々な正の値にしたときの応答特性(振幅のみ)
を様々な正の値にしたときの応答特性(振幅のみ)  フィードフォワード型で
フィードフォワード型で  を様々な負の値にしたときの応答特性(振幅のみ)
を様々な負の値にしたときの応答特性(振幅のみ) Z領域で表される離散時間系の周波数応答を得るには、 と置き換える。すると、フィードフォワード型コムフィルタの伝達関数は次のようになる。
と置き換える。すると、フィードフォワード型コムフィルタの伝達関数は次のようになる。

オイラーの公式を使うと、周波数応答は次のように表すこともできる。
![{\displaystyle \ H(e^{j\omega })=\left[1+\alpha \cos(\omega K)\right]-j\alpha \sin(\omega K)\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/90d3769d0ff3e9a00b58aadf8d0cafb6206b8cb9)
位相を無視して振幅の周波数特性だけを必要とすることが多い。それは次のように定義できる。

フィードフォワード型コムフィルタでは、これが次のようになる。

 という項は定数であり、残る
という項は定数であり、残る  は周期関数である。したがって、コムフィルタの周波数特性は周期的である。
は周期関数である。したがって、コムフィルタの周波数特性は周期的である。
右の2つの図は様々な  の値について、周波数特性の周期性を表したものである。次のような特性が重要である。
の値について、周波数特性の周期性を表したものである。次のような特性が重要である。
- 応答は周期的に局所最小値に落ち込み(「ノッチ」などと呼ぶ)、周期的に局所最大値になる(これを「ピーク」などと呼ぶ)。
- 最大と最小は常に 1 から等しい距離にある。
 のとき、最小の振幅がゼロになる。この場合の局所最小値を「ヌル」などと呼ぶ。
のとき、最小の振幅がゼロになる。この場合の局所最小値を「ヌル」などと呼ぶ。 が正のときの最大と
が正のときの最大と  が負のときの最小は同じ周波数であり、逆も同様である。
が負のときの最小は同じ周波数であり、逆も同様である。
極と零点
再びZ領域でのフィードフォワード型コムフィルタの伝達関数を考える。

見ての通り、 のとき分子がゼロになる。つまり、
のとき分子がゼロになる。つまり、 の解は複素平面上の円周に等間隔で並ぶ。それらが伝達関数の零点である。分母は
の解は複素平面上の円周に等間隔で並ぶ。それらが伝達関数の零点である。分母は  のときゼロとなるので、
のときゼロとなるので、 が一定なら
が一定なら  が極となる。以上から次のような極と零点の図が得られる。
が極となる。以上から次のような極と零点の図が得られる。
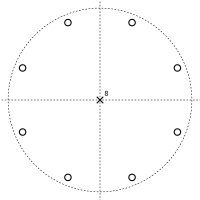  、 、 のときのフィードフォワード型コムフィルタの極(×)と零点(○) のときのフィードフォワード型コムフィルタの極(×)と零点(○) |   、 、 のときのフィードフォワード型コムフィルタの極(×)と零点(○) のときのフィードフォワード型コムフィルタの極(×)と零点(○) |
フィードバック型
 フィードバック型コムフィルタの構造
フィードバック型コムフィルタの構造 フィードバック型コムフィルタの大まかな構造を右図に示す。これは次の式で表せる。
![{\displaystyle \ y[n]=x[n]+\alpha y[n-K]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2658c7503b7bec22305e4b428ad9286da80db066)
 を含む項を左辺に集め、両辺をZ変換すると次のようになる。
を含む項を左辺に集め、両辺をZ変換すると次のようになる。

したがって、伝達関数は次のようになる。

周波数応答
 フィードバック型で
フィードバック型で  を様々な正の値にしたときの応答特性(振幅のみ)
を様々な正の値にしたときの応答特性(振幅のみ)  フィードバック型で
フィードバック型で  を様々な負の値にしたときの応答特性(振幅のみ)
を様々な負の値にしたときの応答特性(振幅のみ) フィードバック型コムフィルタのZ領域表現で  と置き換えると、次の式が得られる。
と置き換えると、次の式が得られる。

振幅の周波数特性は次のようになる。

こちらも周期的な特性となっていることを右の2つの図で示す。フィードバック型コムフィルタはフィードフォワード型と次のような点が共通である。
- 応答は周期的に局所最小値と局所最大値を繰り返す。
 が正のときの最大と
が正のときの最大と  が負のときの最小は同じ周波数であり、逆も同様である。
が負のときの最小は同じ周波数であり、逆も同様である。
しかし、上の式で全ての項が分母にあることから、重要な差異もある。
- 最大値と最小値は 1 から等しい距離にあるわけではない。
 が 1 未満のときだけ安定である。図を見て分かるとおり
が 1 未満のときだけ安定である。図を見て分かるとおり  が大きくなると、最大値の振幅が急激に増大する。
が大きくなると、最大値の振幅が急激に増大する。
極と零点
再びZ領域でのフィードバック型コムフィルタの伝達関数を考える。

この場合、分子がゼロになるのは  のときであり、
のときであり、 が固定なら
が固定なら  が零点となる。分母は
が零点となる。分母は  のときゼロになる。これには
のときゼロになる。これには  個の解があり、複素平面上の円周上に等間隔に並ぶ。それらが伝達関数の極である。以上から次のような極と零点の図が得られる。
個の解があり、複素平面上の円周上に等間隔に並ぶ。それらが伝達関数の極である。以上から次のような極と零点の図が得られる。
  、 、 のときのフィードバック型コムフィルタの極(×)と零点(○) のときのフィードバック型コムフィルタの極(×)と零点(○) | 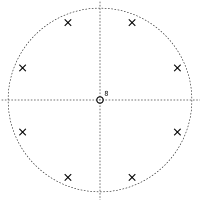  、 、 のときのフィードバック型コムフィルタの極(×)と零点(○) のときのフィードバック型コムフィルタの極(×)と零点(○) |
連続時間コムフィルタ
コムフィルタは連続信号に対しても実装できる。その場合のフィードフォワード型コムフィルタは次の式で表される。

そして、フィードバック型は次の式で表される。

ここで  は遅延である(単位は秒)。
は遅延である(単位は秒)。
これらの周波数特性はそれぞれ次の式になる。


連続信号の場合の特性は離散信号の場合と全く同じである。
関連項目
典拠管理データベース: 国立図書館  | |
|---|










![{\displaystyle \ y[n]=x[n]+\alpha x[n-K]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d27304c28b441814595ccb92181af91876bb8b0c)






![{\displaystyle \ H(e^{j\omega })=\left[1+\alpha \cos(\omega K)\right]-j\alpha \sin(\omega K)\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/90d3769d0ff3e9a00b58aadf8d0cafb6206b8cb9)












![{\displaystyle \ y[n]=x[n]+\alpha y[n-K]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2658c7503b7bec22305e4b428ad9286da80db066)



















