Problema del flusso massimo

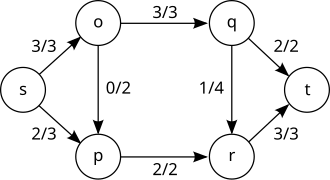
Una rete con un esempio di flusso massimo. La sorgente è s ed il pozzo è t. I numeri denotano flusso e capacità degli archi.

Nella teoria dell'ottimizzazione, il problema del flusso massimo consiste nel trovare, in una rete di flusso con una sola sorgente ed un solo pozzo, un flusso ammissibile che sia massimo.

Il problema del flusso massimo può essere visto come un caso particolare di problemi più complessi sulle reti di flusso, come il problema della circolazione. Il valore massimo di un flusso s-t (ovvero un flusso generato da una sorgente s che si esaurisce in un pozzo t) è equivalente alla capacità minima di un taglio s-t nella medesima rete, come enunciato dal teorema del flusso massimo e taglio minimo.

Storia

Il problema del flusso massimo venne formulato per la prima volta nel 1954 da T. E. Harris e F. S. Ross per la semplificazione del modello del flusso del sistema ferroviario sovietico.[1][2][3] Nel 1955, Lester R. Ford, Jr. e Delbert R. Fulkerson pubblicarono il primo algoritmo noto, l'algoritmo di Ford-Fulkerson.[4][5]

Negli anni a venire, vennero ideate varie soluzioni al problema, fra cui le più note sono quelle degli statunitensi Edmonds e Karp (1972) e del sovietico Dinitz (1970).

Definizione

Una rete di flusso, con sorgente s e pozzo t. I numeri vicini agli archi rappresentano le rispettive capacità.

Sia N = ( V , E ) {\displaystyle N=(V,E)} una rete con s , t ∈ V {\displaystyle s,t\in V} rispettivamente sorgente e pozzo di N {\displaystyle N} .

La capacità di un arco è una funzione c : E → R + {\displaystyle c:E\to \mathbb {R} ^{+}} , indicata con c u v {\displaystyle c_{uv}} o c ( u , v ) {\displaystyle c(u,v)} , che rappresenta il massimo flusso che può passare per un arco.

Un flusso è una funzione f : E → R + {\displaystyle f:E\to \mathbb {R} ^{+}} , indicata con f u v {\displaystyle f_{uv}} o f ( u , v ) {\displaystyle f(u,v)} , soggetta ai due vincoli seguenti:

  1. f u v ≤ c u v ∀ ( u , v ) ∈ E {\displaystyle f_{uv}\leq c_{uv}\forall (u,v)\in E} (vincolo di capacità: il flusso passante in un arco non può essere maggiore della capacità dello stesso);
  2. ∑ u : ( u , v ) ∈ E f u v = ∑ u : ( v , u ) ∈ E f v u ∀ v ∈ V ∖ { s , t } {\displaystyle \sum _{u:(u,v)\in E}f_{uv}=\sum _{u:(v,u)\in E}f_{vu}\forall v\in V\setminus \{s,t\}} (vincolo di conservazione del flusso: la somma dei flussi entranti in un nodo dev'essere uguale alla somma dei flussi uscenti dallo stesso, tranne che per la sorgente ed il pozzo).

Il valore di flusso è definito da | f | = ∑ v : ( s , v ) ∈ E f s v {\displaystyle |f|=\sum _{v:(s,v)\in E}f_{sv}} , dove s {\displaystyle s} è la sorgente di N {\displaystyle N} . Esso rappresenta l'ammontare di flusso che parte dalla sorgente per arrivare al pozzo.

Il problema del flusso massimo è quello di massimizzare | f | {\displaystyle |f|} , ovvero, di instradare quanto più flusso possibile da s {\displaystyle s} a t {\displaystyle t} .

Soluzioni

Per comprendere le varie soluzioni del problema è necessario introdurre il concetto di rete residua. Data una rete di flusso G {\displaystyle G} ed un flusso f {\displaystyle f} su G {\displaystyle G} , definiamo la rete residua G f {\displaystyle G_{f}} su G {\displaystyle G} rispetto a f {\displaystyle f} come segue:

  1. L'insieme dei nodi di G f {\displaystyle G_{f}} è lo stesso di G {\displaystyle G} .
  2. Ogni arco e = ( u , v ) {\displaystyle e=(u,v)} di G f {\displaystyle G_{f}} ha una capacità c e − f ( e ) {\displaystyle c_{e}-f(e)} .
  3. Ogni arco e ′ = ( v , u ) {\displaystyle e'=(v,u)} di G f {\displaystyle G_{f}} ha una capacità f ( e ) {\displaystyle f(e)} .

La seguente tabella elenca gli algoritmi più noti per risolvere il problema del flusso massimo.

Metodo Complessità computazionale Note
Algoritmo di Ford-Fulkerson O ( E   m a x | f | ) {\displaystyle O(E\ max|f|)} La terminazione dell'algoritmo è garantita se tutti i pesi sono razionali, altrimenti è possibile che l'algoritmo non converga al valore massimo. In ogni caso, se l'algoritmo termina, è garantita la correttezza del risultato.
Algoritmo di Edmonds-Karp O ( V E 2 ) {\displaystyle O(VE^{2})} Una specializzazione dell'algoritmo di Ford–Fulkerson sfruttante la ricerca in ampiezza.
Algoritmo di Dinic con flusso bloccante O ( V 2 E ) {\displaystyle O(V^{2}E)} In ogni fase dell'algoritmo viene costruito un grafo stratificato tramite ricerca in ampiezza sul grafo residuo. Il flusso massimo su un grafo stratificato può essere calcolato in tempo O ( V E ) {\displaystyle O(VE)} e il massimo numero di fasi è n − 1 {\displaystyle n-1} . In reti con capacità unitarie l'algoritmo termina in tempo O ( min { V 2 / 3 , E 1 / 2 } E ) {\displaystyle O(\min\{V^{2/3},E^{1/2}\}E)} .
Algoritmo MPM (Malhotra, Pramodh-Kumar e Maheshwari)[6] O ( V 3 ) {\displaystyle O(V^{3})} Ci si riferisca alla pubblicazione originale.
Algoritmo di Dinic O ( V E l o g ( V ) ) {\displaystyle O(VElog(V))} La struttura di albero dinamico velocizza la computazione del flusso massimo nel grafo stratificato fino a O ( E l o g ( V ) ) {\displaystyle O(Elog(V))} .
Algoritmo push-relabel generico O ( V 2 E ) {\displaystyle O(V^{2}E)}
Algoritmo push-relabel con selezione FIFO O ( V 3 ) {\displaystyle O(V^{3})}
Algoritmo push-relabel con alberi dinamici O ( V E log ⁡ V 2 E ) {\displaystyle O\left(VE\log {\frac {V^{2}}{E}}\right)}
Algoritmo KRT (King, Rao, Tarjan)[7] O ( E V log E V log ⁡ V ⁡ V ) {\displaystyle O(EV\log _{\frac {E}{V\log V}}V)}
Algoritmo binario con flusso bloccante[8] O ( E ⋅ min ( V 2 3 , E ) ⋅ log ⁡ V 2 E log ⁡ U ) {\displaystyle O\left(E\cdot \min(V^{\frac {2}{3}},{\sqrt {E}})\cdot \log {\frac {V^{2}}{E}}\log {U}\right)} Il valore U {\displaystyle U} corrisponde alla capacità massima della rete.
Algoritmo di James B Orlin + KRT (King, Rao, Tarjan)[9] O ( V E ) {\displaystyle O(VE)} L'algoritmo di Orlin trova il flusso massimo in tempo O ( V E ) {\displaystyle O(VE)} per E ≤ O ( V 16 15 − ϵ ) {\displaystyle E\leq O(V^{{16 \over 15}-\epsilon })} mentre KRT risolve il problema in O ( V E ) {\displaystyle O(VE)} per E > V 1 + ϵ {\displaystyle E>V^{1+\epsilon }} .

Applicazioni

Sezione vuotaQuesta sezione sull'argomento matematica è ancora vuota. Aiutaci a scriverla!

Note

  1. ^ (EN) A. Schrijver, On the history of the transportation and maximum flow problems, in Mathematical Programming, vol. 91, n. 3, 2002, pp. 437-445, DOI:10.1007/s101070100259.
  2. ^ (EN) Saul I. Gass e Arjang A. Assad, Mathematical, algorithmic and professional developments of operations research from 1951 to 1956, in An Annotated Timeline of Operations Research, International Series in Operations Research & Management Science, vol. 75, 2005, pp. 79-110, DOI:10.1007/0-387-25837-X_5, ISBN 1-4020-8116-2.
  3. ^ (EN) T. E. Harris e F. S. Ross, Fundamentals of a Method for Evaluating Rail Net Capacities (PDF), in Research Memorandum, Rand Corporation, 1955. URL consultato il 31 agosto 2016 (archiviato dall'url originale il 17 febbraio 2017).
  4. ^ (EN) L. R. Ford e D. R. Fulkerson, Maximal flow through a network, in Canadian Journal of Mathematics, vol. 8, 1956, p. 399, DOI:10.4153/CJM-1956-045-5.
  5. ^ (EN) Ford, L.R., Jr.; Fulkerson, D.R., Flows in Networks, Princeton University Press (1962).
  6. ^ (EN) V.M. Malhotra, M.Pramodh Kumar e S.N. Maheshwari, An O ( | V | 3 ) {\displaystyle O(|V|^{3})} algorithm for finding maximum flows in networks, in Information Processing Letters, vol. 7, n. 6, 1978, pp. 277-278, DOI:10.1016/0020-0190(78)90016-9.
  7. ^ (EN) V. King, S. Rao e R. Tarjan, A Faster Deterministic Maximum Flow Algorithm, in Journal of Algorithms, vol. 17, n. 3, 1994, pp. 447-474, DOI:10.1006/jagm.1994.1044.
  8. ^ (EN) A. V. Goldberg e S. Rao, Beyond the flow decomposition barrier, in Journal of the ACM, vol. 45, n. 5, 1998, p. 783, DOI:10.1145/290179.290181.
  9. ^ (EN) James B. Orlin, Max flows in O(nm) time, or better, in STOC '13 Proceedings of the forty-fifth annual ACM symposium on Theory of computing, 2013, pp. 765-774, DOI:10.1145/2488608.2488705.

Bibliografia

  • (EN) Joseph Cheriyan and Kurt Mehlhorn, An analysis of the highest-level selection rule in the preflow-push max-flow algorithm, in Information Processing Letters, vol. 69, n. 5, 1999, pp. 239-242, DOI:10.1016/S0020-0190(99)00019-8.
  • (EN) Daniel D. Sleator and Robert E. Tarjan, A data structure for dynamic trees (PDF), in Journal of Computer and System Sciences, vol. 26, n. 3, 1983, pp. 362-391, DOI:10.1016/0022-0000(83)90006-5, ISSN 0022-0000 (WC · ACNP).
  • (EN) Eugene Lawler, 4. Network Flows, in Combinatorial Optimization: Networks and Matroids, Dover, 2001, pp. 109-177, ISBN 0-486-41453-1.

Voci correlate

Collegamenti esterni

  • Marco Di Summa, Il problema del Flusso Massimo (PDF), su math.unipd.it, Università degli Studi di Padova, Dipartimento di Matematica. URL consultato il 31 agosto 2016 (archiviato il 27 giugno 2013).
  Portale Matematica: accedi alle voci di Wikipedia che trattano di matematica