Produit de Wallis

En mathématiques, le produit de Wallis, ou formule de Wallis, est une expression de la moitié de la constante π sous la forme d'un produit infini, énoncée en 1656 par John Wallis, dans son ouvrage Arithmetica infinitorum.

Expression

Ce produit peut s'écrire sous la forme :

${\displaystyle {\frac {\pi }{2}}={\frac {2}{1}}\times {\frac {2}{3}}\times {\frac {4}{3}}\times {\frac {4}{5}}\times {\frac {6}{5}}\times {\frac {6}{7}}\times {\frac {8}{7}}\times {\frac {8}{9}}\cdots {\frac {2n}{2n-1}}\times {\frac {2n}{2n+1}}\cdots }$

soit, de façon plus condensée :

${\displaystyle {\frac {\pi }{2}}=\prod _{n=1}^{\infty }{\frac {(2n)(2n)}{(2n-1)(2n+1)}}=\prod _{n=1}^{\infty }{\frac {4n^{2}}{4n^{2}-1}}=\prod _{n=1}^{\infty }\left(1+{\frac {1}{4n^{2}-1}}\right)}$

ou encore :

${\displaystyle {\frac {\pi }{2}}=2\prod _{k=1}^{\infty }{\frac {(2k)(2k+2)}{(2k+1)(2k+1)}}=2\prod _{k=1}^{\infty }{\frac {(2k+1)^{2}-1}{(2k+1)^{2}}}=2\prod _{k=1}^{\infty }\left(1-{\frac {1}{(2k+1)^{2}}}\right).}$

Une formulation équivalente est :

${\displaystyle \pi =\lim _{n\rightarrow +\infty }{\frac {1}{n}}{\frac {2^{2}\times 4^{2}\times 6^{2}\cdots (2n)^{2}\,\,\,\,\,\,\,\,\,}{1^{2}\times 3^{2}\times 5^{2}\cdots (2n-1)^{2}}}=\lim _{n\rightarrow +\infty }{\frac {1}{n}}\prod _{k=1}^{n}{\frac {(2k)^{2}}{(2k-1)^{2}}}}$.

Démonstration

On peut démontrer cette égalité à l'aide des intégrales de Wallis.

C'est aussi une conséquence directe de la formule d'Euler-Wallis pour la fonction sinus (qui est un exemple de factorisation de Weierstrass^[1]) :

${\displaystyle {\frac {\sin(x)}{x}}=\prod _{n=1}^{\infty }\left(1-{\frac {x^{2}}{n^{2}\pi ^{2}}}\right)}$

appliquée à x = π/2 :

${\displaystyle {\frac {2}{\pi }}=\prod _{n=1}^{\infty }\left(1-{\frac {1}{4n^{2}}}\right)=\prod _{n=1}^{\infty }{\frac {4n^{2}-1}{4n^{2}}}\quad {\rm {donc}}\quad {\frac {\pi }{2}}=\prod _{n=1}^{\infty }{\frac {4n^{2}}{4n^{2}-1}}}$^[2].

Vitesse de convergence

La vitesse de convergence, lorsque N tend vers l'infini, de la suite des produits finis

${\displaystyle P_{N}=\prod _{n=1}^{N}{\frac {4n^{2}}{4n^{2}-1}}}$

est assez lente, l'écart^[3] avec π/2 étant un O(1/N). Cette suite n'est donc pas utilisée numériquement pour calculer des valeurs approchées de π. La précision peut cependant être améliorée en multipliant P_N par un développement limité dont les premiers termes sont^[4] :

${\displaystyle 1+{\frac {1}{4N}}-{\frac {3}{32N^{2}}}+{\frac {3}{128N^{3}}}+o\left({\frac {1}{N^{3}}}\right).}$

Ainsi, pour N = 10, on obtient :

${\displaystyle P_{N}\simeq 1{,}533851903}$

${\displaystyle \left(1+{\frac {1}{4N}}\right)P_{N}\simeq 1{,}572198201}$

${\displaystyle \left(1+{\frac {1}{4N}}-{\frac {3}{32N^{2}}}\right)P_{N}\simeq 1{,}570760215}$

${\displaystyle \left(1+{\frac {1}{4N}}-{\frac {3}{32N^{2}}}+{\frac {3}{128N^{3}}}\right)P_{N}\simeq 1{,}570796164}$

alors que

${\displaystyle {\frac {\pi }{2}}\simeq 1{,}570796327.}$

Notes et références

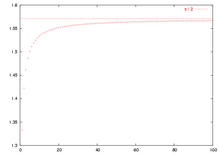
• Portail des mathématiques