Perceptron

Le perceptron est un algorithme d'apprentissage supervisé de classifieurs binaires (c'est-à-dire séparant deux classes). Il a été inventé en 1957 par Frank Rosenblatt^[1] au laboratoire d'aéronautique de l'université Cornell. Il s'agit d'un neurone formel muni d'une règle d'apprentissage qui permet de déterminer automatiquement les poids synaptiques de manière à séparer un problème d'apprentissage supervisé. Si le problème est linéairement séparable, un théorème assure que la règle du perceptron permet de trouver une séparatrice entre les deux classes.

Définition

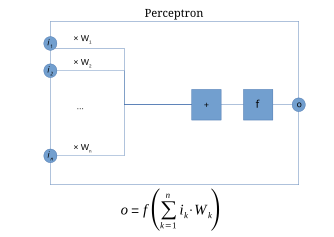
Le perceptron peut être vu comme le type de réseau de neurones le plus simple. C'est un classifieur linéaire. Ce type de réseau neuronal ne contient aucun cycle (il s'agit d'un réseau de neurones à propagation avant). Dans sa version simplifiée, le perceptron est mono-couche et n'a qu'une seule sortie (booléenne) à laquelle toutes les entrées (booléennes) sont connectées. Plus généralement, les entrées peuvent être des nombres réels.

Un perceptron à n entrées ${\displaystyle x=(x_{1},\dots ,x_{n})}$ et à une seule sortie o est défini par la donnée de n poids (aussi appelés coefficients synaptiques^{[réf. nécessaire]}) ${\displaystyle (w_{1},\dots ,w_{n})}$ et un biais (ou seuil) ${\displaystyle \theta }$ par^[2]:

${\displaystyle o=\left\{{\begin{matrix}1&\mathrm {si} &\sum _{i=1}^{n}w_{i}x_{i}\geq \theta \\0&\mathrm {sinon} &\end{matrix}}\right.}$

La sortie o résulte alors de l'application de la fonction de Heaviside au potentiel post-synaptique ${\displaystyle z=\sum _{i=1}^{n}w_{i}x_{i}-\theta }$, où la fonction de Heaviside est :

${\displaystyle \forall z\in \mathbb {R} ,\ H(z)=\left\{{\begin{matrix}0&\mathrm {si} &z<0\\1&\mathrm {si} &z\geq 0.\end{matrix}}\right.}$

On a alors ${\displaystyle o=H(\sum _{i=1}^{n}w_{i}x_{i}-\theta )}$. La fonction ${\displaystyle H}$ est non linéaire et appelée fonction d'activation. Une alternative couramment employée est ${\displaystyle f=\tanh }$, la tangente hyperbolique.

Exemple

La figure de droite montre un perceptron avec 2 entrées ${\displaystyle x}$ et ${\displaystyle y}$. Les poids sont marqués sur les arcs : 1 et 1. Le biais est de 1. Ce perceptron calcule le OU logique de ${\displaystyle x}$ et ${\displaystyle y}$, comme le montre la table suivante :

x	y	x+y	x+y ${\displaystyle \geq }$ 1 ?	valeur de la sortie
0	0	0	non	0
1	0	1	oui	1
0	1	1	oui	1
1	1	2	oui	1

Algorithme d'apprentissage

Notations

Dans la suite de cet article, on considère un échantillon fini de données labélisées ${\displaystyle {\mathcal {S}}=\{(X_{1},y_{1}),~\dots ~,(X_{n},y_{n})\}}$, avec pour tout ${\displaystyle k\in [\![1,\,n]\!]}$, ${\displaystyle X_{k}=(x_{1}^{(k)},\dots ,x_{d}^{(k)},x_{d+1}^{(k)})\in \mathbb {R} ^{d+1}}$, où ${\displaystyle x_{d+1}^{(k)}=1}$^[a], et ${\displaystyle y_{k}\in \{-1,\,1\}}$. On dit alors que les vecteurs ${\displaystyle X_{k}}$ sont les « exemples » et que les points ${\displaystyle y_{k}}$ sont leurs « classes ». Puisque le perceptron ne traite que les problèmes de classification binaire, les ${\displaystyle y_{k}}$ ne peuvent prendre que deux valeurs, par convention ${\displaystyle -1}$ et ${\displaystyle 1}$.

Enfin, on pose ${\displaystyle R=\max _{k\in [\![1,n]\!]}\|X_{k}\|}$, et ${\displaystyle \gamma =\max _{W\in \mathbb {R} ^{d+1}}\min \left\{{\dfrac {y\langle W,X\rangle }{\|W\|}}\,|\,(X,y)\in {\mathcal {S}}\right\}}$.

On suppose également que ${\displaystyle {\mathcal {S}}}$ est linéairement séparable, donc ${\displaystyle \gamma }$ est (strictement) positif. Le fait que ${\displaystyle \gamma }$ soit non-nul découle du lemme suivant :

Lemme de séparabilité linéaire stricte^[3] — S'il existe un hyperplan séparant deux classes de données, alors il existe un hyperplan les séparant et tel qu'aucun exemple ne se trouve dessus, i.e. :

$${\displaystyle \exists (W,b)\in \mathbb {R} ^{d}\times \mathbb {R} ,\,\forall (X_{k},y_{k})\in S,\quad y_{k}(\langle W,X_{k}\rangle +b)>0.}$$

Démonstration^[4] — Soit ${\displaystyle {\mathcal {S}}}$ un échantillon de données labélisées linéairement séparables. Soit ${\displaystyle (W,b)}$ un hyperplan séparant les données de ${\displaystyle {\mathcal {S}}}$. On a alors :

$${\displaystyle {\begin{cases}\langle W,X_{k}\rangle +b\geq 0\quad {\text{si }}y_{k}=1\\\langle W,X_{k}\rangle +b<0\quad {\text{si }}y_{k}=-1.\end{cases}}}$$

Posons ${\displaystyle \varepsilon =-\max _{k}\left\{\langle W,X_{k}\rangle +b\,|\,y_{k}=-1\right\}}$. On a alors :

$${\displaystyle {\begin{cases}\langle W,X_{k}\rangle +b+{\frac {\varepsilon }{2}}\geq {\frac {\varepsilon }{2}}>0\quad {\text{si }}y_{k}=1\\\langle W,X_{k}\rangle +b+{\frac {\varepsilon }{2}}\leq -{\frac {\varepsilon }{2}}<0\quad {\text{si }}y_{k}=-1.\end{cases}}}$$

L'hyperplan ${\displaystyle (W,b+{\frac {\varepsilon }{2}})}$ démontre donc le lemme.

Énoncé

Il existe plusieurs algorithmes d'apprentissage pour un perceptron. L'un des premiers est l'algorithme du perceptron de Rosenblatt, inventé en 1957, qui a pour but de trouver les paramètres d'un hyperplan séparant correctement les deux classes de données^[5],[6] :

Entrées : un échantillon ${\displaystyle {\mathcal {S}}=\{(X_{1},y_{1}),~\dots ~,(X_{n},y_{n})\}}$de données labélisées
Sortie : la matrice ${\displaystyle W}$ de poids telle que ...[Quoi ?]
1 Initialiser ${\displaystyle W=0_{\mathbb {R} ^{d+1}}}$
2 Répéter
3    Pour ${\displaystyle i=1}$ à ${\displaystyle n}$
4        Si ${\displaystyle y_{i}\langle W,X_{i}\rangle \leq 0}$ alors
5            ${\displaystyle W\leftarrow W+y_{i}X_{i}}$
6    Fin pour
7 jusqu'à ce qu'il n'y ait plus d'erreurs
8 Retourner ${\displaystyle W}$

L'algorithme du perceptron de Rosenblatt est un cas particulier de l'algorithme du gradient stochastique utilisant comme fonction objectif ${\displaystyle C(W)=\sum _{i\in {\mathcal {M}}}y_{i}\langle W,X_{i}\rangle }$, où ${\displaystyle {\mathcal {M}}}$ est l'ensemble des exemples mal classés ; et un taux d'apprentissage de ${\displaystyle 1}$^[7].

Convergence

La convergence de l'algorithme est démontrée en 1962 par Novikoff.

Démonstration^[10] — On note ${\displaystyle (W_{k})}$ la suite des valeurs prises par ${\displaystyle W}$ lors de l'exécution de l'algorithme. On a donc ${\displaystyle W_{1}=0}$. On suppose que l'algorithme fait ${\displaystyle k}$ erreurs, et que la ${\displaystyle k}$-ième erreur est faite sur l'exemple ${\displaystyle X_{t}}$. On note ${\displaystyle W^{*}}$ les paramètres d'un hyperplan classant correctement tous les exemples, avec ${\displaystyle \|W^{*}\|=1}$.

On a donc, en appliquant l'algorithme :

$${\displaystyle {\begin{aligned}\langle W_{k+1},W^{*}\rangle &=\langle W_{k}+y_{t}X_{t},W^{*}\rangle \\&=\langle W_{k},W^{*}\rangle +y_{t}\langle X_{t},W^{*}\rangle \\&\geq \langle W_{k},W^{*}\rangle +\gamma \\&\geq k\gamma \end{aligned}}}$$

La troisième ligne découle de la définition de ${\displaystyle \gamma }$. La quatrième ligne s'obtient par récurrence, puisque ${\displaystyle W_{1}=0}$. Or, d'après l'inégalité de Cauchy-Schwarz, ${\displaystyle \|W_{k+1}\|~\|W^{*}\|\geq \langle W_{k+1},W^{*}\rangle }$, et ${\displaystyle \|W^{*}\|=1}$ donc, ${\displaystyle \|W_{k+1}\|\geq k\gamma }$.

De plus :

$${\displaystyle {\begin{aligned}\|W_{k+1}\|^{2}&=\|W_{k}+y_{t}X_{t}\|^{2}\\&=\|W_{k}\|^{2}+y_{t}^{2}\|X_{t}\|^{2}+2y_{t}\langle X_{t},W_{k}\rangle \\&\leq \|W_{k}\|^{2}+R^{2},\end{aligned}}}$$

puisque ${\displaystyle y_{t}^{2}\|X_{t}\|^{2}=\|X_{t}\|^{2}\leq R^{2}}$ et ${\displaystyle y_{t}\langle X_{t},W_{k}\rangle \leq 0}$, car l'algorithme se trompe sur le ${\displaystyle t}$-ième exemple à la ${\displaystyle k}$-ième itération. Finalement, on obtient par récurrence que : ${\displaystyle \|W_{k+1}\|^{2}\leq kR^{2}}$.

Donc, ${\displaystyle k^{2}\gamma ^{2}\leq \|W_{k+1}\|^{2}\leq kR^{2}}$. On en déduit enfin que ${\displaystyle k\leq (R/\gamma )^{2}}$.

Lorsque les données entrées ne sont pas linéairement séparables, l'algorithme ne converge pas, et la suite ${\displaystyle (W_{k})}$ est périodique. Le cycle peut cependant être long et difficile à détecter.

Règle de Hebb

La règle de Hebb, établie par Donald Hebb^[11], est une règle d'apprentissage des réseaux de neurones artificiels dans le contexte de l'étude d'assemblées de neurones.

Cette règle suggère que lorsque deux neurones sont excités conjointement, ils créent ou renforcent un lien les unissant.

Dans le cas d'un neurone artificiel seul utilisant la fonction signe comme fonction d'activation cela signifie que :

${\displaystyle W'_{i}=W_{i}+\alpha (Y.X_{i})}$

où ${\displaystyle W'_{i}}$ représente le poids ${\displaystyle i}$ corrigé et ${\displaystyle \alpha }$ représente le pas d'apprentissage.

Cette règle n'est malheureusement pas applicable dans certains cas bien que la solution existe.

Règle d'apprentissage du perceptron (loi de Widrow-Hoff)

Le perceptron de Frank Rosenblatt est très proche de la règle de Hebb, la grande différence étant qu'il tient compte de l'erreur observée en sortie.

Cette fonction est recommandée lorsque la tangente hyperbolique (tanh) est utilisée comme fonction d'activation.

${\displaystyle W'_{i}=W_{i}+\alpha (Y_{t}-Y)X_{i}}$

avec :

• ${\displaystyle W'_{i}}$ = le poids ${\displaystyle i}$ corrigé ;
• ${\displaystyle Y_{t}}$ = sortie attendue ;
• ${\displaystyle Y}$ = sortie observée ;
• ${\displaystyle \alpha }$ = le taux d'apprentissage ;
• ${\displaystyle X_{i}}$ = l'entrée du poids ${\displaystyle i}$ pour la sortie attendue ${\displaystyle Y_{t}}$ ;
• ${\displaystyle W_{i}}$ = le poids ${\displaystyle i}$ actuel.

Notes et références

Notes

Références

Voir aussi

• Réseau neuronal artificiel
• Perceptron multicouche

Bibliographie

• F. Rosenblatt (1958), The perceptron: a probabilistic model for information storage and organization in the brain,

- repris dans J.A. Anderson & E. Rosenfeld (1988), Neurocomputing. Foundations of Research, MIT Press

• Trevor Hastie, Robert Tibshirani et Jerome Friedman, The Elements of Statistical Learning : Data Mining, Inference, and Prediction, Second Edition, Springer New York, 2009, (ISBN 978-0-387-84858-7).

• Portail des probabilités et de la statistique
• Portail de l’informatique
• Portail de l'informatique théorique