Ondelette de Haar

Cet article est une ébauche concernant les mathématiques.

Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants.

L'ondelette de Haar, ou fonction de Rademacher, est une ondelette créée par Alfréd Haar en 1909^[1]. On considère que c'est la première ondelette connue. Il s'agit d'une fonction constante par morceaux, ce qui en fait l'ondelette la plus simple à comprendre et à implémenter. L'ondelette de Haar peut être généralisée par ce qu'on appelle le système de Haar.

Ondelette de Haar

La fonction-mère des ondelettes de Haar est une fonction constante par morceaux :

${\displaystyle \psi (t)={\begin{cases}1&\quad {\textrm {pour}}\;\;0\leq t<{\frac {1}{2}},\\-1&\quad {\textrm {pour}}\;\;{\frac {1}{2}}\leq t<1,\\0&\quad {\textrm {sinon}}\\\end{cases}}}$

La fonction d'échelle associée est alors une fonction porte :

${\displaystyle f(t)={\begin{cases}1&\quad {\textrm {pour}}\;\;0\leq t<1,\\0&\quad {\textrm {sinon}}\\\end{cases}}}$

Le système de Haar

Le système de Haar est une suite de fonctions continues par morceaux, appartenant à ${\displaystyle L^{p}([0,1])}$ pour ${\displaystyle 1\leq p<+\infty }$. Il est défini de la manière suivante, à partir des fonctions indicatrices :

• ${\displaystyle h_{1}(t)=1\!\!1_{[0;1]}(t)}$

• Pour ${\displaystyle k\geq 0}$ et ${\displaystyle 1\leq l\leq 2^{k}}$ :

${\displaystyle h_{2^{k}+l}(t)=1\!\!1_{\left[{\frac {2l-2}{2^{k+1}}};{\frac {2l-1}{2^{k+1}}}\right]}(t)-1\!\!1_{\left[{\frac {2l-1}{2^{k+1}}};{\frac {2l}{2^{k+1}}}\right]}(t).}$

Voici les représentations graphiques de h₂ et de h₃ :

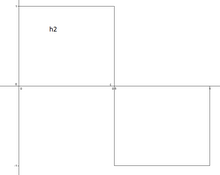
Une des propriétés intéressantes du système de Haar est qu'il est une base de Schauder de ${\displaystyle L^{p}([0,1])}$ pour ${\displaystyle 1\leq p<+\infty }$ .

Références

Articles connexes

• Caractéristiques pseudo-Haar
• Base de Hilbert
• Voir aussi la catégorie « Ondelette »

• Portail de l'analyse