Fonction booléenne

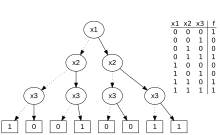
Une fonction booléenne est une fonction prenant en entrée une liste de bits et donnant en sortie un unique bit.

Les fonctions booléennes sont très utilisées en informatique théorique, notamment en théorie de la complexité et en cryptologie (par exemple dans les boîtes-S et les chiffrements par flot -- fonction de filtrage ou de combinaison de registres à décalage à rétroaction linéaire).

Définition, exemple et circuits

Une fonction booléenne est une fonction de ${\displaystyle \mathbb {F} ^{n}}$ dans ${\displaystyle \mathbb {F} }$ où ${\displaystyle \mathbb {F} }$ désigne le corps fini à 2 éléments. Un exemple de fonction booléenne est la fonction parité, dont la sortie dépend de la parité du nombre de 1 dans l'entrée. Une fonction booléenne peut être représentée par un circuit booléen.

Propriétés

Forme algébrique normale

Les corps finis et les polynômes interpolateurs de Lagrange conduisent rapidement à une propriété fondamentale des fonctions booléennes : la représentation dite « forme algébrique normale » (algebraic normal form ou ANF). Toute fonction booléenne peut s'écrire comme un polynôme en ${\displaystyle n}$ variables à coefficients dans ${\displaystyle \mathbb {F} }$. Cependant, différents polynômes de ${\displaystyle \mathbb {F} [X_{0},...,X_{n-1}]}$ donnent la même fonction. Par exemple, ${\displaystyle X_{0}^{2}}$ et ${\displaystyle X_{0}^{3}}$ donnent bien la même valeur lorsqu'ils sont évalués sur un élément de ${\displaystyle \mathbb {F} ^{n}}$. Pour obtenir une représentation unique, il faut considérer les éléments de l'anneau quotient, soit :

${\displaystyle \mathbb {F} [X_{0},...,X_{n-1}]/(X_{0}^{2}+X_{0},...,X_{n-1}^{2}+X_{n-1})}$

Autrement dit, une fonction booléenne peut être représentée de manière unique par un polynôme de la forme :

${\displaystyle P(X_{0},...,X_{n-1})=\sum _{u_{j}=(u_{j_{0}},...,u_{j_{n-1}})\in \mathbb {F} ^{n}}a_{u_{j}}\prod _{i=0}^{n-1}X_{i}^{u_{j_{i}}}}$

(${\displaystyle u_{j}}$ est une suite d'éléments de ${\displaystyle \mathbb {F} }$ et ${\displaystyle a_{u_{j}}\in \mathbb {F} }$).

On pose fréquemment ${\displaystyle u=(u_{j_{0}},...,u_{j_{n-1}})~}$, ${\displaystyle X=(X_{0},...,X_{n-1})~}$ et ${\displaystyle X^{u}=\prod _{i=0}^{n-1}X_{i}^{u_{i}}}$, permettant l'écriture compacte :

${\displaystyle P(X)=\sum _{u\in \mathbb {F} ^{n}}a_{u}X^{u}}$.

La notion de degré d'une fonction booléenne est alors évidente, il s'agit du degré maximal des monômes de son ANF.

Exemple de forme algébrique normale sur ${\displaystyle \mathbb {F} ^{3}}$ :

${\displaystyle P([X_{1},X_{2},X_{3}])=X_{1}X_{2}+X_{1}X_{3}+X_{2}X_{3}}$

Linéarité et non-linéarité

Les fonctions de degré 1 sont appelées les fonctions affines. En fait, ce sont des formes affines de l'espace vectoriel ${\displaystyle \mathbb {F} ^{n}}$ — vu comme espace sur le corps ${\displaystyle \mathbb {F} }$. Ce sont les fonctions les plus simples, hormis les constantes. Il a fini par apparaître que « ressembler » à une fonction linéaire était une propriété pouvant être exploitée en cryptanalyse. La ressemblance en question se base sur le nombre de fois où deux fonctions prennent la même valeur, il s'agit de la distance de Hamming :

${\displaystyle d_{H}(f,g)=\#\{u\in \mathbb {F} ^{n}:f(u)\neq g(u)\}}$

Les cryptographes utilisent le terme de non-linéarité pour parler de la distance d'une fonction booléenne à l'ensemble ${\displaystyle {\mathcal {A}}}$ des fonctions affines :

${\displaystyle {\mathcal {N}}(f)=\min\{d_{H}(f,g):g\in {\mathcal {A}}\}}$

L'intérêt de cette notion est de quantifier l'erreur commise si on remplace la fonction ${\displaystyle f}$ par une fonction affine : dans le meilleur des cas, on se « trompe » ${\displaystyle {\mathcal {N}}(f)}$ fois sur ${\displaystyle 2^{n}}$ si ${\displaystyle n}$ est le nombre de variables.

On montre, en utilisant la transformée de Fourier, que la non-linéarité d'une fonction booléenne est au plus de

${\displaystyle {\mathcal {N}}(f)\leq 2^{n-1}-2^{{\frac {n}{2}}-1}}$

Lorsque ${\displaystyle n}$ est pair, cette borne supérieure est atteinte, on parle alors de fonction courbe.

Précisons que l'ensemble des fonctions affines a une importance particulière en théorie des codes correcteurs, au point qu'il possède un nom, le code de Reed-Muller d'ordre 1 (en ${\displaystyle n}$ variables). L'ordre est le degré maximal des fonctions. Ainsi, le code de Reed-Muller d'ordre ${\displaystyle r~}$ en ${\displaystyle n~}$, usuellement noté ${\displaystyle \mathrm {RM} (r,n)~}$ est l'ensemble des fonctions en ${\displaystyle n~}$ variables de degré au plus ${\displaystyle r~}$. Dans le contexte de la théorie des codes, la non-linéarité maximale se trouve correspondre au « rayon de recouvrement » du code ${\displaystyle \mathrm {RM} (1,n)~}$, c'est-à-dire la distance maximale entre un mot binaire de longueur ${\displaystyle 2^{n}}$ et un mot du code.

Outil d'étude : la transformée de Fourier

La transformation de Fourier, appliquée aux fonctions booléennes, se révèle être un moyen très puissant pour explorer les différentes propriétés de ces objets. Elle est, par exemple, fréquemment utilisée pour étudier des propriétés cryptographiques comme la non-linéarité maximale. On la retrouve également dans des aspects plus appliquées : l'existence d'algorithmes de calcul de la transformée de Fourier de type FFT sert à décoder efficacement les codes de Reed et Muller. On trouvera dans la suite une présentation générale de la transformation de Fourier dans le cas des groupes abéliens finis qui est ensuite particularisée pour le cas des fonctions booléennes.

Cas d'un groupe abélien fini

Dans le cas d'un groupe abélien fini, le théorème de Kronecker assure que le groupe est isomorphe à un produit direct de groupes cycliques. Ce théorème est à la base de nombreuses propriétés des fonctions booléennes.

Caractère et groupe dual

De manière générale, on peut définir une transformation de Fourier sur un groupe ${\displaystyle {\mathcal {G}}}$ en utilisant la notion de caractère. Un caractère ${\displaystyle \chi }$ est un morphisme de ${\displaystyle {\mathcal {G}}}$ dans ${\displaystyle \mathbb {U} }$, le groupe des racines de l'unité du corps des nombres complexes ${\displaystyle \mathbb {C} }$.

L'ensemble des caractères opèrent sur l'ensemble des applications de ${\displaystyle {\mathcal {G}}}$ dans ${\displaystyle \mathbb {C} }$, cet ensemble est appelé algèbre du groupe et est généralement noté ${\displaystyle \mathbb {C} [{\mathcal {G}}]}$. Il est muni du produit hermitien suivant :

${\displaystyle \forall \chi _{1},\chi _{2}\in \mathbb {C} [{\mathcal {G}}]\quad \langle \chi _{1}|\chi _{2}\rangle ={\frac {1}{|{\mathcal {G}}|}}\sum _{g\in {\mathcal {G}}}\chi _{1}(g)^{*}.\chi _{2}(g)}$

Ici si z est un complexe, z^* désigne son conjugué.

Les caractères forment une base orthonormale de l'algèbre du groupe.

L'ensemble des caractères de ${\displaystyle {\mathcal {G}}}$ peut être muni d'une structure de groupe en utilisant la multiplication entre applications, ce groupe est appelé le groupe dual. Le groupe ${\displaystyle {\mathcal {G}}}$ et son dual sont isomorphes si ${\displaystyle {\mathcal {G}}}$ est abélien.

Les démonstrations sont données dans l'article détaillé.

Définition de la transformée de Fourier

Lorsque ${\displaystyle {\mathcal {G}}}$ est abélien et fini, il est possible de définir simplement la transformée de Fourier. On appelle transformée de Fourier d'un élément de l'algèbre du groupe de ${\displaystyle {\mathcal {G}}}$ une application du groupe dual ${\displaystyle {\mathcal {F}}({\mathcal {G}})}$ dans ${\displaystyle \mathbb {C} }$ notée ici ${\displaystyle {\mathcal {F}}(f)}$ et définie par :

${\displaystyle \forall \chi \in {\mathcal {F}}({\mathcal {G}})\quad {\mathcal {F}}(f)(\chi )={\frac {1}{\sqrt {|{\mathcal {G}}|}}}\sum _{x\in {\mathcal {G}}}f(x)\chi (x)^{*}}$

Cette application dispose de toutes les propriétés usuelles d'une transformée de Fourier, elle est linéaire, l'égalité de Parseval le théorème de Plancherel, la formule sommatoire de Poisson et la dualité de Pontryagin sont par exemple vérifiées. Il est aussi possible de définir un produit de convolution.

Les démonstrations sont données dans l'article détaillé.

Espace vectoriel fini

Il existe un cas important, celui où le groupe est un espace vectoriel fini V, donc de dimension fini sur un corps fini ${\displaystyle \mathbb {K} }$. Dans ce cas, il existe un isomorphisme entre V et son groupe dual, appelé dualité de Pontryagin. Soit . une forme bilinéaire non dégénérée de V et μ un caractère non trivial de ${\displaystyle \mathbb {K} }$, l'application χ de V dans son dual, qui à y associe le caractère χ_y définie par l'égalité suivante est cet isomorphisme :

${\displaystyle \forall x\in V\quad \chi _{y}(x)=\mu (y.x)}$

Cet isomorphisme permet d'exprimer la transformation de Fourier d'un élément f de l'algèbre du groupe de V de la manière suivante :

${\displaystyle \forall \zeta \in V\quad {\mathcal {F}}(f)(\zeta )={\frac {1}{\sqrt {|V|}}}\sum _{x\in V}f(x)\mu (-\zeta .x)}$

Espace vectoriel sur le corps F₂

Formes des caractères et isomorphisme avec le dual

On considère maintenant le cas où le corps ${\displaystyle \mathbb {K} }$ est celui à deux éléments noté ${\displaystyle \mathbb {F} _{2}}$ et l'espace vectoriel est ${\displaystyle \mathbb {F} _{2}^{n}}$ où n est un entier strictement positif. Soit x = (x_i) et y = (y_i) deux éléments de l'espace vectoriel, la forme bilinéaire . est définie par :

${\displaystyle x.y=\sum _{i=1}^{n}x_{i}.y_{i}}$

Il n'existe que deux caractères dans ${\displaystyle \mathbb {F} _{2}}$, le caractère trivial et celui qui à s associe (-1)^s. Comme il n'existe qu'un caractère non trivial, l'isomorphisme χ du paragraphe précédent prend la forme suivante :

${\displaystyle \forall x,y\in \mathbb {F} _{2}^{n}\quad \chi _{y}(x)=(-1)^{x.y}}$

Transformation de Walsh

Dans le cas d'un espace vectoriel binaire (ie. sur le corps fini à deux éléments) la transformée de Fourier prend le nom de transformée de Walsh. Elle prend la forme suivante :

${\displaystyle \forall y\in \mathbb {F} _{2}^{n}\quad {\hat {f}}(y)={\mathcal {F}}(f)(\chi _{y})={\frac {1}{\sqrt {2^{n}}}}\sum _{x\in {\mathbb {F} ^{n}}}f(x){(-1)}^{x\cdot y}}$

On remarque que le signe moins utilisé dans la définition disparait car dans ${\displaystyle \mathbb {F} _{2}}$ la multiplication par -1 est égale à l'identité. On remarque que la transformée de Walsh est idempotente, c'est-à-dire qu'elle est égale à son inverse.

On voit donc que l'un des intérêts de cette identification est d'avoir la transformation de Walsh et son inverse qui agissent sur les mêmes objets : des fonctions de ${\displaystyle \mathbb {F} ^{n}}$ dans ${\displaystyle {\mathbb {C} }}$.

Formule de Poisson

Un autre intérêt de l'identification de ${\displaystyle \mathbb {F} _{2}^{n}}$ et de son dual, et non moins agréable que celui évoqué précédemment, est de simplifier considérablement la formule de Poisson. En effet, on obtient alors

${\displaystyle \sum _{u\in a+{\mathcal {H}}^{\bot }}{\hat {f}}(u){(-1)}^{u\cdot b}={(-1)}^{a\cdot b}|H^{\bot }|\cdot \sum _{u\in b+{\mathcal {H}}}f(u)(-1)^{a\cdot u}}$

On remarque que ${\displaystyle {\mathcal {H}}^{\bot }}$ s'identifie naturellement à ${\displaystyle \{z\in \mathbb {F} _{2}^{n}:\forall x\in H,z\cdot x=0\}}$. C'est ce qui est fait dans la formule ci-dessus, passant ainsi d'une notation multiplicative pour ${\displaystyle {\mathcal {H}}^{\bot }}$ à une notation additive (on a également utilisé ${\displaystyle b=-b}$ dans le cas de ${\displaystyle \mathbb {F} _{2}^{n}}$). On vérifie également que ${\displaystyle {\mathcal {H}}}$ et ${\displaystyle {\mathcal {H}}^{\bot }}$ sont des espaces vectoriels sur ${\displaystyle \mathbb {F} _{2}}$.

Voir aussi

Liens externes

• Christine Bachoc, « Cours de code », sur université Bordeaux I, 2004-2005
• Christine Bachoc, « Mathématiques discrètes de la transformée de Fourier », sur université Bordeaux I, 2004-2005
• A. Bechata, « Analyse harmonique sur les groupes finis commutatifs »
• R. Rolland, « Groupes finis commutatifs et transformation de Fourier discrète », sur Institut de mathématiques de Luminy

Bibliographie

• Michel Demazure, Cours d'algèbre : primalité, divisibilité, codes [détail des éditions]
• (en) Thomas W. Cusick et Pantelimon Stanica, Cryptographic Boolean Functions and Applications, Academic Press, 2009
• (en) Jessie MacWilliams et Neil Sloane, The Theory of Error-Correcting Codes, North-Holland, 1977 (ISBN 978-0-444-85009-6)
• André Warusfel, Structures algébriques finies, Éditions Hachette, 1971
• G. Peyré, L'algèbre discrète de la transformée de Fourier, Éditions Ellipses, 2004

• Portail des mathématiques
• Portail de la cryptologie
• Portail de l'informatique théorique