De prospectiva pingendi

De Prospectica pingendi
Première page du codex de Bordeaux.
Auteur	Piero della Francesca
Pays	Italie
Genre	codex
Version originale
Langue	Toscan et latin
Titre	De Prospectiva Pingendi
Date de parution	circa 1475
modifier

De Prospectiva pingendi (« De la perspective en peinture ») est un traité sur la théorie de la perspective écrit par Piero della Francesca. La datation en est incertaine, mais se situe entre les années 1460 et 1480. Cette œuvre, l'un des traités fondateurs de l'art de la Renaissance, a un ton beaucoup plus pratique et moins vers le particulier que le traité De pictura (1435) de Leon Battista Alberti. Le texte, sans fioritures philosophiques ni théologiques, se concentre sur les aspects mathématiques et géométriques, avec des applications pratiques spécifiques, dans un style sobre et clair.

Importance du livre

Avec son traité De Prospectiva pingendi, Piero della Francesca a changé le cours des techniques artistiques de la représentation des objets à trois dimensions sur une surface à deux dimensions. Avant lui, des précurseurs comme Filippo Brunelleschi, Cennino Cennini et Leon Battista Alberti avaient donné des prémisses de techniques pour la représentation d'objets tri-dimensionnels. Les rapports entre Piero della Francesca et Alberti sont analysés par J.V. Field^[1].

Malgré le titre de son ouvrage, Piero ne traite pas seulement de la représentation en perspective d'objets en trois dimensions (la perspective linéaire), mais également de la représentation orthogonale, et il peut être considéré comme le fondateur de la géométrie descriptive élaboré par Gaspard Monge au début du XIX^e siècle^[2] et du Dessin technique.

Le traité de Piero della Francesca est unique dans le sens qu'il présente à la fois les bases théoriques et procédures mathématiques pour achever les diminutions correctes dans les projections spatiales et une série d'exercices, de difficulté croissante, pour instruire l'artisan-peintre. Pour les artisans il y a une explication verbale, une illustration graphique des méthodes et la langue originale du premier codex écrite en langue vernaculaire (le toscan). D'autres codices, destinés aux élites, étaient écrits en latin.

De Prospectiva pingendi s'est répandu dans les différents ateliers artistiques au travers d'une série de codices manuscrits et son contenu a été incorporé dans presque tous les œuvres postérieures qui traitent de la représentation d'objets en trois dimensions en peinture et architecture.

Les manuscrits et les traductions

Le traité fut très probablement écrit dans les années 1474-1475, même si plusieurs modifications mineures conservées dans les codices successifs suggèrent une gestation probable depuis le milieu des années 1460.

Piero della Francesca écrivit en langue vernaculaire, le toscan et Maestro Matteo di Ser Paolo a traduit le codex en latin « de verbo ad verbum »^[3].

Le traité a survécu en sept codices, tous ont été numérisés et sont consultables en-ligne.

Le codex en italien de Reggio Emilia et les codices en latin de Milan et Bordeaux sont probablement contemporains (on y retrouve en fait la main du même copiste). La version italienne la plus proche de l'original est celle de Reggio Emilia (sans les additions).

Éditions critiques et facsimilés

• Édition en allemand du codex :(de) Piero della Francesca (trad. Constantin Winterberg), Petrus pictor Burgensis de prospectiva pingendi, Heitz & Mündel, 1899, 396 p. (disponible sur Internet Archive).

• Édition en français du codex de Parma : Piero della Francesca (trad. de l'italien par Jean-Pierre Le Goff et Jean-Pierre Néraudau, préf. Hubert Damisch, postface Daniel Arasse), De la perspective en peinture : Ms Parmensis, 1576 [« De prospectiva pingendi »], Paris, Éditions In Medias Res, 1998 (1^re éd. 1576), 351 p. (ISBN 2-9511719-0-0).

• (it) Piero della Francesca, A. Menghini (dir.) et D. Contin (dir.), De prospectiva pingendi (Facsimilé du manuscrit originel), Aboca Edizioni, 2009, 225 p. (ISBN 978-88-95642-30-7).

• Édition en italien, du MS vernaculaire de Chiara Gizzi : (it) Chiara Gizzi, « Piero Della Francesca - De Prospectiva pingendi » [PDF], Edizioni Ca’Foscari, 2016 (consulté le 9 septembre 2018)^[12].

Contenu du livre

De Prospectiva pingendi est le premier traité sur les mathématiques des techniques de représentation d'objet à trois dimensions sur une surface de deux dimensions. Piero avait deux buts : la représentation d'un objet tel qu'il « est réellement » et la représentation d'un objet tel que l'on le « voit réellement ».

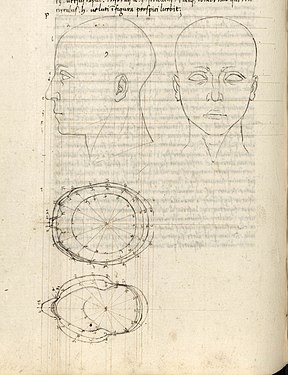
Dans le premier cas par exemple, des lignes parallèles ne se rencontrent jamais, et dans le deuxième si, sur la ligne de l'horizon au point de fuite. Les premiers méthodes forment la base du dessin technique et sont illustrées par la représentation de la tête humaine ci-dessous.

La perspective linéaire est une méthode pour représenter une réalité parmi d'autres, avec des avantages et des inconvénients. En particulier il y a la limitation du champ vu. Une personne qui regarde le tableau doit se placer à la position de l'artiste et si le champ vu est large, le tableau, vu d'une autre position comportera beaucoup de distorsion.

L'utilisation de la perspective, par un artiste très habile, peut donner une impression d'« irréalité » à un tableau. Par exemple, Piero dans sa fresque la Résurrection utilise deux points de fuite : avec le premier le spectateur regarde les soldats d'en bas et avec le deuxième il regarde le Christ d'en haut. Le résultat contribue à l'aspect surnaturel de l’œuvre.

Le principe de base était décrit par Leon Battista Alberti : les rayons lumineux provenant d'une scène forment des lignes droites à partir des points de la scène jusqu'à l’œil de l'artiste. Ils forment une sorte de pyramide, avec l’œil placé à l'apex. Le tableau de l'artiste doit représenter une section de cette pyramide coupée par un plan. L'application de ce principe constitue la majeure partie du traité.

Cette idée est simple, mais elle n'indique pas « comment » représenter cette section de la pyramide sur le tableau. Le traité de Piero est le premier à donner des constructions géométriques précises pour accomplir ce travail.

L'ouvrage est divisé en trois livres :

• I : décrivant comment il faut dessiner les objets individuellement,
• II : décrivant comment les placer dans l'espace,
• III : la représentation d'objets complexes.

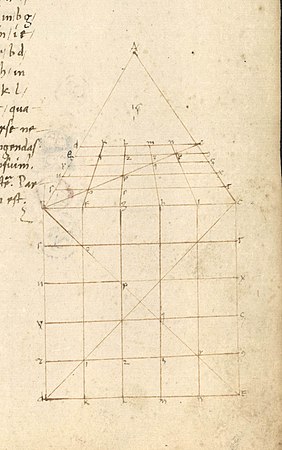
Les légendes des illustrations sont aussi importantes que le texte écrit et les problèmes suivent une progression croissante, allant du plus simple au plus complexe de façon très méthodique. Le traité est conçu comme un manuel pratique pour apprendre aux peintres et aux architectes comment dessiner en perspective, avec des dizaines d'exercices, illustrés de diagrammes^[13].

Pour Piero la représentation des objets est basée sur la théorie de la vision exposée dans l'Optique d'Euclide.

Dans le premier livre il commence par exposer les idées de Euclide. Puis il passe à la représentation de figures simples :

• Un carré sur le sol ; l'observateur à une hauteur et distance donnée ; quelle est la figure que l'artiste doit dessiner sur son tableau ?
• La même question pour une série de carrés qui forment le carrelage d'une pièce ou pour un polygone quelconque au sol.

Le deuxième livre est un pas vers les objets plus compliqués.

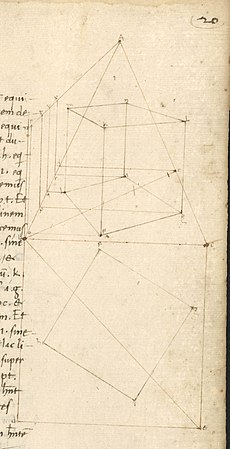
• Une fois que l'on sait dessiner des polygones au sol, on les érige en cubes, prismes etc.
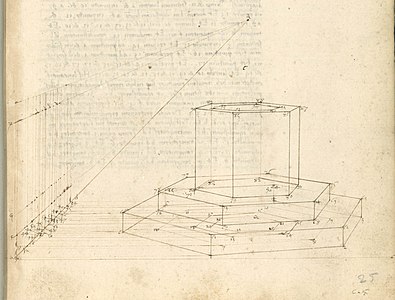
• Quand on maitrise la représentation des prismes, on passe aux bâtiments sur plan carré, rectangulaire, circulaire, des coupoles, etc.

Le troisième livre est consacré à des objets complexes : chapiteaux, corps humains etc. avec des représentations en projection orthogonales et en perspective.

Le traité est d'abord destiné aux artisans-peintres et architectes, pas aux mathématiciens. Donc, pour les premiers Piero présente une série de « recettes » : « Pour dessiner un carré en perspective, faites ça, ça et ça... pour obtenir le résultat ». Cependant, Piero est un mathématicien et pour lui la démonstration de ses constructions est essentielle et il les donne, mais parfois de façon laconique.

Sa construction fondamentale pour le dessin d'un carré est donné, et démontré, dans la proposition 13. Quand on a bien compris cette preuve, il est relativement facile à compléter les démonstrations des constructions ultérieures.

Un exemple typique de l'application de la théorie exposé dans De Prospectiva pingendi est le tableau La Cité idéale, commandé par le duc d'Urbino vers 1480. L'auteur est inconnu, mais probablement un architecte. Il a très bien assimilé les méthodes de Piero exposées dans De Prospectiva pingendi.

Les mathématiques du livre

À son époque Piero était reconnu comme un mathématicien très compétent. Giorgio Vasari dans Les Vies des meilleurs peintres, sculpteurs et architectes dit que Piero a montré une aptitude pour les mathématiques depuis son enfance et qu'il a écrit « beaucoup » de traités de mathématiques. De ses traités seulement deux autres sont parvenus à nous : Trattato d'abaco et Libellus de quinque corporibus regularibus (voir Piero le mathématicien).

De Prospectiva pingendi ne doit pas être juste considéré comme seulement un manuel d'exercices de dessin. Il comporte aussi des mathématiques très originales :

• Un «  théorème fondamental  » (le seul exercice qui n'a pas d'illustration), mais qui est central au sujet^[2].
• La démonstration de Piero de sa construction pour la représentation en perspective d'un carré par terre est la première nouvelle addition à la géométrie de Euclide depuis Fibonacci au XII^e siècle et marque le début de la géométrie projective.

Dans le livre I, après quelques constructions élémentaires pour introduire l'idée que la dimension apparente d'un objet est mesurée par l'angle sous-tendu à l’œil et avec référence Euclide, I à VI et à son livre Optiques, nous arrivons au problème 13 de Piero : « Comment représenter un carré, à terre devant l'observateur ? »

« Que doit dessiner exactement l'artiste ou l'architecte ? »

Dès que la solution de cette question basique est bien assimilée, Piero passe à la représentation d'autres polygones posés à terre, avec n'importe quelle orientation.

La technique de base est la représentation en perspective du carré, toutes les autres représentations en découlent.

La construction de Piero pour le carré en perspective

Fig. A

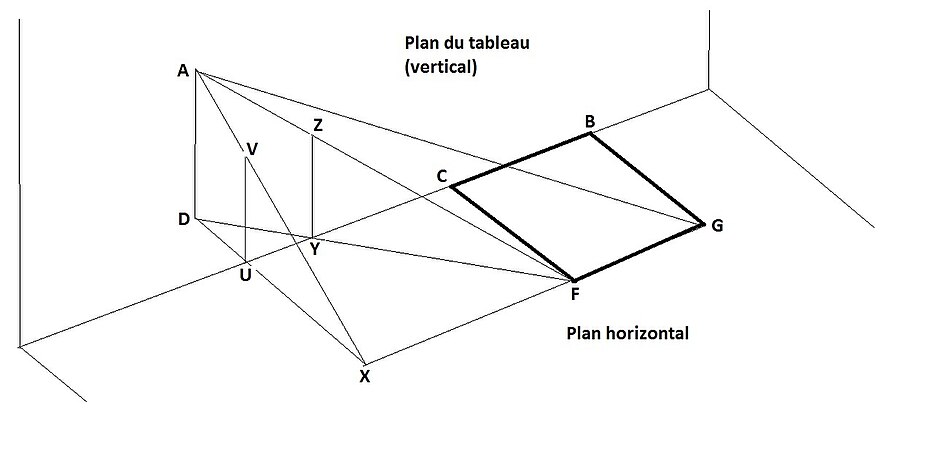
La situation basique est illustrée dans la figure ci-contre :

• Un carré (noir) est posé par terre horizontalement ;
• L’œil de l'artiste, ${\displaystyle A}$, situé un peu à droit du carré, l'observe d'une certaine distance et d'une certaine hauteur ;
• Son canevas est à la verticale, devant le carré.

Que doit-il dessiner sur le canevas pour représenter ce qu'il voit du carré ?

Le principe du dessin en perspective est de tracer des lignes droites entre chaque point du carré et l’œil de l'artiste. Les points d'intersection de ces lignes avec le plan du canevas donne la représentation du carré ${\displaystyle BCE'D'}$, vu par l'artiste.

Le dessin de la perspective n'est pas un dessin à « main-levée », c'est une construction géométrique très précise, surtout pour des représentations architecturales. Les longueurs apparentes des lignes doivent être reproduites avec exactitude.

La construction que l'artiste doit faire est dans le plan de son tableau. Les lignes auxiliaires nécessaires pour déterminer la représentation seront effacées, ou, si c'est un dessin préliminaire, le résultat sera calqué sur le tableau définitif. Dans tous les cas, l'artiste doit représenter sur son dessin toutes les dimensions (côté du carré, distance de l'artiste, hauteur de l'artiste) à l'échelle. Ci-dessous est l’algorithme de Piero ; on peut le suivre, obtenir le carré en perspective sans comprendre le « pourquoi » de son efficacité.

L'algorithme de Piero

L'illustration de Piero Fig. B : L'algorithme de Piero

Dans le plan du tableau, tracez :

1. le carré ${\displaystyle BCGF}$ que l'on veut représenter en perspective ;
2. la ligne ${\displaystyle DBC}$ telle que ${\displaystyle BD}$ est la distance entre l'artiste et la côté du carré au sol ;
3. la ligne verticale ${\displaystyle DA}$, tel que ${\displaystyle DA}$ est la hauteur de l’œil de l'artiste au-dessus du sol ;
4. la ligne parallèle à ${\displaystyle DBC}$ qui passe par ${\displaystyle A}$ ; sur cette ligne marquez le point ${\displaystyle A'}$, qui représente la position latérale de l'artiste par rapport au carré sur le sol ;
5. la ligne ${\displaystyle AC}$, qui coupe ${\displaystyle BF}$ en ${\displaystyle E}$ ;
6. la ligne ${\displaystyle AG}$ qui coupe ${\displaystyle BF}$ en ${\displaystyle H}$ ;
7. les lignes ${\displaystyle A'B}$ et ${\displaystyle A'C}$ ;
8. une ligne parallèle à ${\displaystyle CBD}$ qui passe par ${\displaystyle E}$ et coupe ${\displaystyle A'B}$ en ${\displaystyle D'}$ et ${\displaystyle A'C}$ en ${\displaystyle E'}$.

Le quadrilatère ${\displaystyle BCE'D'}$ est la représentation en perspective du carré au sol devant l'artiste.

La construction de Piero est simple, concise, ingénieuse, et surtout, élégante. Elle était conçue par un mathématicien de grand talent.

On peut répéter la construction facilement pour représenter, par exemple le carrelage d'une salle en perspective. On n'a nullement besoin de comprendre la démonstration car la construction donne le résultat escompté en suivant simplement la « recette ».

L’apparition du « carré en perspective » à la suite de ces opérations est un peu surprenant. Comment s'assurer que cette représentation est correcte ?

Pour comprendre la construction de Piero il faut faire la même gymnastique intellectuelle que lui.

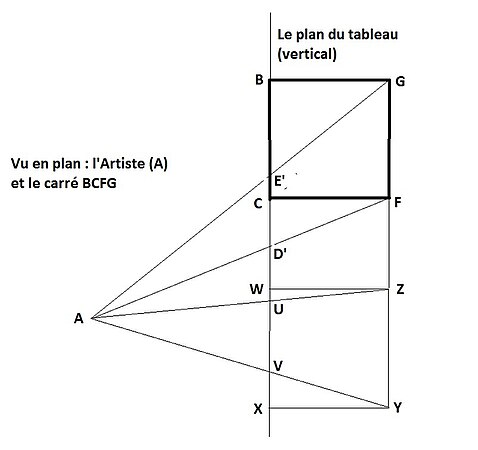
D'abord on doit se rendre compte que la Fig. B est la somme de deux vues orthogonales de la situation représentée dans Fig. A et le tableau vu par l'artiste :

• La vue orthogonale, parallèle au plan du tableau, qui sera utilisée pour déterminer la hauteur du carré dans la représentation en perspective.
• La vue orthogonale, en plan, qui sera utilisée pour déterminer la longueur de la côté du carré la plus éloigné de l'artiste.
• La vue finale du tableau, avec la représentation du carré en perspective.

Dans la construction il y a trois questions importantes :

• Pourquoi la longueur ${\displaystyle BE}$ du segment est elle égale à la hauteur de la représentation du carré dans le tableau ?
• Pourquoi la longueur du segment ${\displaystyle EH}$ est-elle égale à la longueur du côté du carré le plus éloigné de l'artiste ?
• Pourquoi les deux longueurs ${\displaystyle EH}$ et ${\displaystyle D'E'}$ sont-elles égales ?

Les démonstrations de Piero sont basées sur une série de relations, très ingénieuses, entre des triangles similaires. Il utilise le théorème de Thalès, qui affirme que les rapports entre les côtés correspondantes de deux triangles similaires sont constants.

La démonstration que ${\displaystyle BE}$ est la hauteur du carré en perspective

Fig. C

Dans la figure ci-contre :

Si nous plaçons ${\displaystyle X}$ tel que ${\displaystyle DX}$ est perpendiculaire au plan du tableau, nous sommes dans la situation de l'étape 5 de l'algorithme, ou la ligne ${\displaystyle AC}$ coupe ${\displaystyle BF}$ en ${\displaystyle E}$.

La hauteur du carré en perspective dans le plan du tableau est ${\displaystyle YZ}$ ; nous démontrons que ${\displaystyle YZ=UV}$. La correspondance avec la construction de Piero est que le triangle ${\displaystyle ADX}$ corresponde au triangle${\displaystyle ADC}$ et ${\displaystyle UV}$ à ${\displaystyle BE}$.

• Les triangles ${\displaystyle ADF}$ et ${\displaystyle ZYF}$ sont similaires. Par le théorème de Thales : ${\displaystyle {\frac {ZY}{AD}}={\frac {DY}{DF}}}$.
• Les triangles ${\displaystyle DFX}$ et ${\displaystyle DYU}$ sont similaires. Par le théorème de Thales : ${\displaystyle {\frac {DY}{DF}}={\frac {DU}{DX}}}$.
• Les triangles ${\displaystyle ADX}$ et ${\displaystyle VUX}$ sont similaires. Par le théorème de Thales : ${\displaystyle {\frac {UV}{AD}}={\frac {DU}{DX}}}$.

Donc ${\displaystyle {\frac {UV}{AD}}={\frac {YZ}{AD}}}$ et ${\displaystyle UV=YZ}$.

Q.E.D.

 

La démonstration que ${\displaystyle EH}$ est la longueur de la côté du carré la plus éloigné de l'artiste

Fig. D

Dans l'étape 6 de sa construction Piero regarde la figure dans le plan du tableau comme étant vu à la verticale et il applique la méthode ci-dessus pour construire le segment ${\displaystyle EH}$ qui a la longueur requise.

La figure ci-contre est une vue orthogonale, en plan, de la situation représentée en Fig. A.

La position du côté ${\displaystyle FG}$ du carré dans le plan du tableau est donné par l'intersection des lignes ${\displaystyle AG}$ et ${\displaystyle AF}$ avec le plan du tableau, c'est-à-dire le segment ${\displaystyle E'D'}$ (lignes noire grasse). Il faut la longueur de ${\displaystyle E'D'}$.

Piero sait que s'il glisse une copie (${\displaystyle WXYZ}$) du carré contre le plan du tableau et trace les lignes ${\displaystyle AY}$ et ${\displaystyle AZ}$, alors le segment ${\displaystyle UV}$ a la même longueur que le segment ${\displaystyle E'D'}$. Le carré ${\displaystyle WXYZ}$ correspond au carré ${\displaystyle BCFG}$ dans la Fig. A.

Démonstration :

• Les triangles ${\displaystyle AFG}$ et ${\displaystyle AWD'}$ sont similaires. Par le théorème de Thales : ${\displaystyle {\frac {E'D'}{GF}}={\frac {AD'}{AF}}}$.
• Les triangles ${\displaystyle AZF}$ et ${\displaystyle AD'E'}$ sont similaires. Par le théorème de Thales : ${\displaystyle {\frac {AD'}{AF}}={\frac {AW}{AZ}}}$.
• Les triangles ${\displaystyle AYZ}$ et ${\displaystyle AVU}$ sont similaires. Par le théorème de Thales : ${\displaystyle {\frac {AW}{AZ}}={\frac {UV}{YZ}}}$.

Alors, ${\displaystyle {\frac {D'E'}{GF}}={\frac {UV}{YZ}}}$, mais ${\displaystyle GF=YZ}$, qui implique ${\displaystyle D'E'=UV}$

Q.E.D.

 

La démonstration que ${\displaystyle EH=D'E'}$

Fig.E

Démonstration :

Les triangles similaires utilisés sont :

• Les triangles ${\displaystyle A'BC}$ et ${\displaystyle A'D'E'}$ sont similaires, donc ${\displaystyle {\frac {D'E'}{BC}}={\frac {A'E'}{A'C}}}$
• Les triangles ${\displaystyle AA'C}$ et ${\displaystyle EE'C}$ sont similaires, donc ${\displaystyle {\frac {A'E'}{A'C}}={\frac {AE}{AC}}}$
• Les triangles ${\displaystyle AHE}$ et ${\displaystyle ACG}$ sont similaires, donc ${\displaystyle {\frac {AE}{AC}}={\frac {EH}{CG}}}$

Donc, ${\displaystyle {\frac {D'E'}{BC}}={\frac {A'E'}{A'C}}={\frac {AE}{AC}}={\frac {EH}{CG}}}$ et parce que ${\displaystyle BC=CG}$ on a ${\displaystyle D'E'=EH}$.

Q.E.D.

 

 

Références

Annexes

Bibliographie

 : document utilisé comme source pour la rédaction de cet article..

• Lucien Vinciguerra, Archéologie de la perspective : Sur Piero della Francesca, Vinci et Dürer, Paris, Presses Universitaires de France, coll. « Lignes d'art », 2007, 163 p. (ISBN 978-2-13-056000-5).
• (en) The Cambridge Companion to Piero della Francesca (dir.), The Cambridge Companion to Piero della Francesca, Cambridge University Press, coll. « Cambridge Companions to the History of Art », 2002, 310 p. (ISBN 978-0-521-65472-2).

• (en) Kirsti Andersen, « The Mathematical Treatment of Anamorphoses from Piero della Francesca to Niceron », dans History of Mathematics: States of the Art. Flores Quadrivii – Studies in the Honor of Christoph J. Scriba, Academic Press, 1996.

• (en) Kirsti Andersen, The Geometry of an Art : The history of the mathematical theory of perspective from Alberti to Monge, Berlin, Springer, 2008, 814 p. (ISBN 978-0-387-25961-1, présentation en ligne).

• (en) Marco Bussagli (trad. de l'italien), Piero Della Francesca, Giunti Editore, coll. « Art Dossier Series », 1998, 60 p. (ISBN 978-88-09-21559-7, présentation en ligne).

• (en) Judith Veronica Field (dir.), « Mathematics and the craft of painting : Piero della Francesca and Perspective », dans J.V. Field and Frank A.J.L. James, Renaissance et Revolution : Humanists, scholars, craftsmen and natural philosophers in early modern Europe, Cambridge University Press, 1997, 2^e éd. (1^re éd. 1993) (ISBN 0-521-43427-0, présentation en ligne).

• (en) Judith Veronica Field, « A Mathematician's Art », dans M.A. Lavin, Piero della Francesca and His Legacy, Washington, National Gallery of Art, 1995, 328 p. (ISBN 9780894682032), p. 177-198.

• (en) Martin Kemp, « Piero and the Idiots: The Early Fortuna of His Theories of Perspective », dans M.A. Lavin, Piero della Francesca and His Legacy, Washington, National Gallery of Art, 1995, 328 p. (ISBN 9780894682032), p. 199-212.

• (en) Judith Veronica Field, The Invention of Infinity : Mathematics and Art in the Renaissance, Oxford University Press, 1997, 262 p. (ISBN 978-0-19-852394-9, présentation en ligne).
• (en) Mark A. Peterson, « The Geometry of Piero della Francesca », sur Mount Holyoke College et (en) Mark A. Peterson, « The Geometry of Piero della Francesca », The Mathematical Intelligencer, vol. 19, n^o 3,‎ juin 1997, p. 33-40 (DOI 10.1007/BF03025346, présentation en ligne).
• (en) Judith Veronica Field, Piero Della Francesca : A Mathematician's Art, Yale University Press, 2005, 420 p. (ISBN 978-0-300-10342-7, présentation en ligne).
• (en) Larry Witham, Piero's Light : In search of Piero della Francesca, a Renaissance painter and the revolution in Art, Science and Religion, Open Road Media, 2014, 400 p. (ISBN 978-1-60598-494-0, présentation en ligne).

• Jean-Pierre Crettez, Les supports de la géométrie interne des peintres : De Cambue à Georges de La Tour, ISTE éditions, coll. « Arts et Savoirs », 2017, 536 p. (ISBN 978-1-78405-223-2, présentation en ligne), p. 319- 384 - Chapitre 7 : Trois œuvres de Piero della Francesca.

Articles connexes

Liens externes

• Portail de la littérature italienne
• Portail de l’histoire de l’art
• Portail de la peinture
• Portail de la Renaissance
• Portail de la langue latine