Courbe implicite

En mathématiques, une courbe implicite (en coordonnées cartésiennes) est une courbe plane définie par une équation implicite reliant les deux coordonnées x et y d'un point de ${\displaystyle {\mathbb {R}}^{2}}$. Par exemple, le cercle unité est défini par l'équation implicite ${\displaystyle x^{2}+y^{2}=1}$. Dans le cas général, une courbe implicite est définie en coordonnées cartésiennes par une équation de la forme

${\displaystyle F(x,y)=0}$

où F est une fonction de deux variables. Elle peut donc être considérée comme l'ensemble des zéros d'une telle fonction. Implicite signifie que l'équation n'est pas sous une forme où y a été explicité en fonction de x, ou l'inverse.

Si ${\displaystyle F}$ est un polynôme à deux variables, la courbe correspondante est dite algébrique, et il existe des méthodes spécifiques pour l'étudier.

Les courbes planes peuvent être représentées en coordonnées cartésiennes sous trois formes, dont l'une est la forme implicite vue ci-dessus, une autre, la forme explicite ${\displaystyle y=f(x)}$ (ou ${\displaystyle x=f(y)}$), et la troisième, la forme paramétrique, où les coordonnées x et y sont représentées par deux fonctions x(t), y(t) dépendant d'un paramètre commun ${\displaystyle t.}$

En pratique les courbes implicites ont pour inconvénient principal une visualisation difficile. Mais il existe des programmes informatiques permettant de les représenter. Les propriétés particulières des courbes implicites en font des outils indispensables en géométrie et en infographie.

Exemples

Voici des exemples de courbes implicites :

1. une droite : ${\displaystyle x+2y-3=0,}$
2. un cercle : ${\displaystyle x^{2}+y^{2}-4=0,}$
3. la parabole semi-cubique : ${\displaystyle x^{3}-y^{2}=0,}$
4. les ovales de Cassini :${\displaystyle (x^{2}+y^{2})^{2}-2c^{2}(x^{2}-y^{2})-(a^{4}-c^{4})=0}$ (voir figure ci-dessus),
5. ${\displaystyle \sin(x+y)-\cos(xy)+1=0}$ (voir figure).

Les quatre premiers exemples sont algébriques, mais pas le dernier. Les courbes des trois premiers exemples possèdent des représentations paramétriques simples, ce qui n'est pas le cas des quatrième et cinquième exemples. Ce dernier montre que la structure géométrique d'une courbe implicite peut éventuellement être complexe.

Une courbe implicite d'équation ${\displaystyle F(x,y)=0}$ peut être considérée comme la courbe de niveau 0 de la surface ${\displaystyle z=F(x,y)}$ (voir la troisième figure).

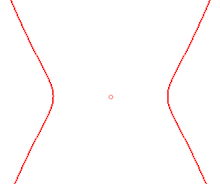
Courbes équipotentielles de deux charges ponctuelles

Les courbes équipotentielles de deux charges ponctuelles égales aux points ${\displaystyle P_{1}=(1,0),\;P_{2}=(-1,0)}$ sont représentées par l'équation

${\displaystyle {\begin{aligned}f(x,y)&={\frac {1}{|PP_{1}|}}+{\frac {1}{|PP_{2}|}}-c\\[3pt]&={\frac {1}{\sqrt {(x-1)^{2}+y^{2}}}}+{\frac {1}{\sqrt {(x+1)^{2}+y^{2}}}}-c=0.\end{aligned}}}$

Les courbes ressemblent aux ovales de Cassini, mais ce n'en sont pas.

Pente et courbure

Le théorème des fonctions implicites explicite les conditions sous lesquelles une équation ${\displaystyle F(x,y)=0}$ peut être résolue implicitement en x et/ou y – c'est-à-dire qu'on peut valablement écrire ${\displaystyle y=f(x)}$ ou ${\displaystyle x=f(y)}$. Ce théorème est la clé du calcul des caractéristiques géométriques essentielles de la courbe : tangentes, normales et courbure.

En général, les courbes implicites échouent au test de la droite verticale (ce qui signifie que certaines valeurs de x sont associées à plusieurs valeurs de y ) et ne sont donc pas nécessairement des graphes de fonctions. Cependant, le théorème des fonctions implicites donne des conditions sous lesquelles une courbe implicite est représentée localement par le graphe d'une fonction (en particulier si elle n'a pas d'auto-intersections). Si les relations de définition sont suffisamment lisses, alors, dans de telles régions, les courbes implicites ont des pentes, des tangentes, des vecteurs normaux et une courbure bien définis.

Il existe plusieurs manières de calculer ces quantités pour une courbe implicite donnée. Une méthode consiste à utiliser la différenciation implicite pour calculer les dérivées de y par rapport à x. Pour une courbe définie par l'équation implicite ${\displaystyle F(x,y)=0}$, on peut aussi exprimer ces formules directement en termes de dérivées partielles de ${\displaystyle F}$ . Dans ce qui suit, les dérivées partielles sont notées ${\displaystyle F_{x}}$ ou p (pour la dérivée par rapport à x), ${\displaystyle F_{y}}$ ou q, ${\displaystyle F_{xx}}$ ou r (pour la dérivée seconde partielle par rapport à x), ${\displaystyle F_{xy}}$ ou s (pour la dérivée seconde partielle mixte), et ${\displaystyle F_{yy}}$ ou t.

Vecteur tangent et vecteur normal

Un point ${\displaystyle (x_{0},y_{0})}$ de la courbe est dit régulier si l'une des dérivées partielles premières ${\displaystyle F_{x}(x_{0},y_{0})}$ et ${\displaystyle F_{y}(x_{0},y_{0})}$ est non nulle, autrement dit si${\displaystyle {\text{grad}}F(x_{0},y_{0})\neq (0,0)}$.

L'équation de la tangente en un point régulier ${\displaystyle (x_{0},y_{0})}$ est donnée par :

${\displaystyle F_{x}(x_{0},y_{0})(x-x_{0})+F_{y}(x_{0},y_{0})(y-y_{0})=0}$,

donc la pente de la tangente, si ${\displaystyle F_{y}(x_{0},y_{0})\neq 0,}$ est égale à

${\displaystyle -{\frac {F_{x}(x_{0},y_{0})}{F_{y}(x_{0},y_{0})}}}$.

Dans le cas où ${\displaystyle F_{y}(x_{0},y_{0})=0\neq F_{x}(x_{0},y_{0})}$, la courbe est verticale en ce point.

Un vecteur normal à la courbe en ce point est donné par

${\displaystyle \mathbf {n} (x_{0},y_{0})=(F_{x}(x_{0},y_{0}),F_{y}(x_{0},y_{0}))}$.

Courbure en un point régulier

Pour la lisibilité des formules, les arguments ${\displaystyle (x_{0},y_{0})}$ sont omis. La courbure ${\displaystyle \kappa }$ en un point régulier est donnée par la formule

${\displaystyle \kappa =-{\frac {F_{y}^{2}F_{xx}-2F_{x}F_{y}F_{xy}+F_{x}^{2}F_{yy}}{(F_{x}^{2}+F_{y}^{2})^{3/2}}}=-{\frac {q^{2}r-2pqs+p^{2}t}{(p^{2}+q^{2})^{3/2}}}=-{\frac {{\begin{bmatrix}-q&p\end{bmatrix}}{\begin{bmatrix}r&s\\s&t\end{bmatrix}}{\begin{bmatrix}-q\\p\end{bmatrix}}}{(p^{2}+q^{2})^{3/2}}}}$^[1].

Obtention des formules précédentes

Si ${\displaystyle F_{y}(x_{0},y_{0})\neq 0,}$ le théorème des fonctions implicites garantit au voisinage d'un point ${\displaystyle (x_{0},y_{0})}$ l'existence d'une fonction ${\displaystyle f}$ telle que ${\displaystyle F(x,f(x))=0}$ . Par la règle de dérivation des fonctions composées, les dérivées de la fonction ${\displaystyle f}$ sont alors :

${\displaystyle f'(x)=-{\frac {F_{x}(x,f(x))}{F_{y}(x,f(x))}}}$ et ${\displaystyle f''(x)=-{\frac {F_{y}^{2}F_{xx}-2F_{x}F_{y}F_{xy}+F_{x}^{2}F_{yy}}{F_{y}^{3}}}}$

(où les arguments ${\displaystyle (x,f(x))}$ à droite de la deuxième formule sont omis pour faciliter la lecture).

Or les formules de la pente de tangente et de la courbure ${\displaystyle \kappa (x_{0})}$ de la courbe d'équation explicite ${\displaystyle y=f(x)}$ sont respectivement

${\displaystyle \left\{{\begin{array}{c}f'(x_{0})\\{\frac {f''(x_{0})}{(1+f'(x_{0})^{2})^{3/2}}}\end{array}}\right.}$

D'où les résultats du paragraphe précédent en insérant les valeurs ci-dessus, résultats encore valables si ${\displaystyle F_{y}(x_{0},y_{0})=0\neq F_{x}(x_{0},y_{0})}$.

Cas d'un point singulier

Si les deux dérivées ${\displaystyle F_{x}(x_{0},y_{0})}$ et ${\displaystyle F_{y}(x_{0},y_{0})}$ sont nulles, la courbe y présente un point singulier.

Si en ${\displaystyle (x_{0},y_{0})}$ , ${\displaystyle \det {\begin{bmatrix}r&s\\s&t\end{bmatrix}}=rt-s^{2}>0}$, il s'agit d'un point isolé.

Si en ${\displaystyle (x_{0},y_{0})}$ , ${\displaystyle \det {\begin{bmatrix}r&s\\s&t\end{bmatrix}}=rt-s^{2}<0}$, il s'agit d'un point de croisement.

Si en ${\displaystyle (x_{0},y_{0})}$ , ${\displaystyle \det {\begin{bmatrix}r&s\\s&t\end{bmatrix}}=rt-s^{2}=0}$, il s'agit en général d'un point de rebroussement.

Avantages et inconvénient des courbes implicites

Avantages

1. Les représentations implicites facilitent le calcul des points d'intersection : si une courbe est représentée implicitement et l'autre paramétriquement, le calcul des points d'intersection ne nécessite qu'une simple itération de Newton (à une dimension) (mais pas dans les cas implicite-implicite et paramétrique-paramétrique).
2. Une représentation implicite ${\displaystyle F(x,y)=0}$ donne la possibilité de créer des zones hors de la courbe suivant le signe de ${\displaystyle F(x,y)}$. Cela peut être utile par exemple pour appliquer la méthode de la fausse position au lieu d'une itération de Newton.
3. Il est facile de générer des courbes qui sont presque géométriquement semblables à la courbe implicite donnée ${\displaystyle F(x,y)=0,}$ en ajoutant juste une petite constante : ${\displaystyle F(x,y)-c=0}$ (voir le paragraphe Approximations lisses ).

Inconvénient

L'inconvénient principal du fait qu'une courbe soit sous forme implicite est l'absence de possibilité facile de calcul de points donnés, ce qui est nécessaire pour la visualisation de cette courbe (voir le paragraphe de visualisation).

Applications des courbes implicites

En mathématiques, les courbes implicites jouent un rôle important en tant que courbes algébriques. De plus, des courbes implicites sont utilisées pour concevoir des courbes de formes souhaitée ; voici deux exemples.

Approximations lisses

Une approximation lisse d'un polygone convexe peut être obtenue de la manière suivante : Soit ${\displaystyle g_{i}(x,y)=a_{i}x+b_{i}y+c_{i}=0,\ i=1,\dotsc ,n}$ les équations des droites contenant les bords du polygone, exprimées de façon que pour un point intérieur au polygone ${\displaystyle g_{i}}$ soit positif. Un sous-ensemble de la courbe implicite

${\displaystyle F(x,y)=g_{1}(x,y)\cdots g_{n}(x,y)-c=0}$

avec un petit paramètre approprié ${\displaystyle c}$ est alors une approximation lisse (différentiable) du polygone. Par exemple, les courbes

${\displaystyle F(x,y)=(x+1)(-x+1)y(-x-y+2)(x-y+2)-c=0}$ pour ${\displaystyle c=0,03\ ;\dotsc ;0,6}$

contiennent des approximations lisses d'un polygone à 5 côtés (voir figure).

Couples de droites

Dans le cas de deux droites

${\displaystyle F(x,y)=g_{1}(x,y)g_{2}(x,y)-c=0}$

on obtient

• un faisceau de droites parallèles, si les droites données sont parallèles ou
• un faisceau d'hyperboles ayant pour asymptotes les droites données.

Par exemple, le produit des variables des axes de coordonnées donne le faisceau des hyperboles ${\displaystyle xy-c=0,\ c\neq 0}$, ayant les axes de coordonnées comme asymptotes.

Autres cas

Si l'on part de simples courbes implicites autres que des droites (cercles, paraboles,...) on obtient un large éventail de nouvelles courbes intéressantes. Par exemple,

${\displaystyle F(x,y)=y(-x^{2}-y^{2}+1)-c=0}$

(produit d'un cercle et de l'axe des x) donne des approximations lisses du bord d'un demi-disque (voir image), et

${\displaystyle F(x,y)=(-x^{2}-(y+1)^{2}+4)(-x^{2}-(y-1)^{2}+4)-c=0}$

(produit de deux cercles) donne des approximations lisses du bord de l'intersection de deux disques (voir image).

Courbes de raccord

En CAO on utilise des courbes implicites pour générer des courbes de raccord^[2],[3], qui sont des courbes établissant une transition douce entre deux courbes données. Par exemple,

${\displaystyle F(x,y)=(1-\mu )f_{1}f_{2}-\mu (g_{1}g_{2})^{3}=0}$

génère des courbes de raccord entre les deux cercles

${\displaystyle f_{1}(x,y)=(x-x_{1})^{2}+y^{2}-r_{1}^{2}=0,}$

${\displaystyle f_{2}(x,y)=(x-x_{2})^{2}+y^{2}-r_{2}^{2}=0.}$

La méthode garantit la continuité des tangentes et des courbures aux points de contact (voir schéma). Les deux droites

${\displaystyle g_{1}(x,y)=x-x_{1}=0,\ g_{2}(x,y)=x-x_{2}=0}$

déterminent les points de contact aux cercles. Le paramètre ${\displaystyle \mu }$ est un paramètre de conception. Dans la figure, ${\displaystyle \mu =0,05\ ;\dotsc \ ;0,2}$ .

Visualisation d'une courbe implicite

Pour visualiser une courbe implicite, on détermine généralement une suite de points sur la courbe et on affiche le polygone correspondant. Pour une courbe paramétrique, c'est une tâche facile : on calcule simplement les points d'une suite de valeurs du paramètre. Pour une courbe implicite, il faut résoudre deux sous-problèmes :

1. déterminer un premier point de courbe à un point de départ donné au voisinage de la courbe,
2. déterminer un point de la courbe à partir d'un point de la courbe connu.

Dans les deux cas, il est raisonnable de supposer ${\displaystyle \operatorname {grad} F\neq (0,0)}$ . En pratique, cette hypothèse n'est violée qu'en des points isolés.

Algorithme ponctuel

Pour la solution des deux tâches mentionnées ci-dessus, il est indispensable de disposer d'un programme informatique (que nous appellerons ${\displaystyle {\mathsf {CPoint}}}$ ), qui, lorsqu'on lui donne un point ${\displaystyle Q_{0}=(x_{0},y_{0})}$ près d'une courbe implicite, trouve un point ${\displaystyle P}$ qui est exactement sur la courbe:

(P1) pour le point de départ, ${\displaystyle j=0}$

(P2) répéter

${\displaystyle (x_{j+1},y_{j+1})=(x_{j},y_{j})-{\frac {F(x_{j},y_{j})}{F_{x}(x_{j},y_{j})^{2}+F_{y}(x_{j},y_{j})^{2}}}\,\left(F_{x}(x_{j},y_{j}),F_{y}(x_{j},y_{j})\right)}$

(méthode de Newton pour la fonction ${\displaystyle g(t)=F\left(x_{j}+tF_{x}(x_{j},y_{j}),y_{j}+tF_{y}(x_{j},y_{j})\right)\ .}$ )

(P3) jusqu'à la distance entre les points ${\displaystyle (x_{j+1},y_{j+1}),\,(x_{j},y_{j})}$ est assez petite.

(P4) ${\displaystyle P=(x_{j+1},y_{j+1})}$ est le point de la courbe près du point de départ ${\displaystyle Q_{0}}$ .

Algorithme de traçage

Afin de générer un polygone dont les sommets sont quasi également espacés sur la courbe implicite, on choisit une longueur de pas ${\displaystyle s}$ et

(T1) on choisit un point de départ approprié à proximité de la courbe

(T2) on détermine un premier point de courbe ${\displaystyle P_{1}}$ en utilisant le programme ${\displaystyle {\mathsf {CPoint}}}$

(T3) on détermine la tangente (voir ci-dessus), on choisit un point de départ sur la tangente en utilisant la longueur du pas ${\displaystyle s}$ (voir schéma) et on détermine un deuxième point de courbe ${\displaystyle P_{2}}$ en utilisant le programme ${\displaystyle {\mathsf {CPoint}}}$ .

${\displaystyle \cdots }$

L'algorithme ne trace que des composantes connexes de la courbe. Si elle en possède plusieurs, il doit être redémarré plusieurs fois avec des points de départ appropriés.

Algorithme de rastérisation

Si la courbe implicite est constituée de plusieurs composantes, il peut être préférable d'utiliser un algorithme de rastérisation. Au lieu de suivre exactement la courbe, un tel algorithme couvre toute la courbe par beaucoup de points de sorte qu'ils se mélangent et fassent ressortir la courbe.

(R1) Générer un réseau de points (un raster) sur la zone d'intérêt du plan xy.

(R2) Pour chaque point ${\displaystyle P}$ dans le réseau, exécuter l'algorithme de point ${\displaystyle {\mathsf {CPoint}}}$ à partir de ${\displaystyle P}$, puis marquer sa sortie.

Si le réseau est suffisamment dense, le résultat se rapproche de la courbe implicite.

Courbes implicites en coordonnées polaires

Une courbe implicite en coordonnées polaires est définie par une équation du type ${\displaystyle G(\rho ,\theta )=0}$. Le passage de l'équation cartésienne ${\displaystyle F(x,y)=0}$ d'une courbe, à son équation polaire se fait facilement en posant ${\displaystyle G(\rho ,\theta )=F(\rho \cos \theta ,\rho \sin \theta )}$ ; le passage inverse, plus délicat, se fait en utilisant les relations ${\displaystyle \rho ^{2}=x^{2}+y^{2}}$ et ${\displaystyle y\cos \theta =x\sin \theta }$.

Par exemple, la courbe implicite cartésienne ${\displaystyle (3x^{2}-y^{2})^{2}y^{2}-(x^{2}+y^{2})^{4}=0}$ ci-contre a pour équation polaire ${\displaystyle \rho \pm \sin 3\theta =0}$.

Dans le repère polaire, la tangente a pour pente ${\displaystyle {\frac {\rho }{\frac {d\rho }{d\theta }}}=-{\frac {\rho G_{\rho }}{G_{\theta }}}}$.

Courbes implicites 3D

Une courbe de l'espace définie par deux équations

${\displaystyle {\begin{matrix}F(x,y,z)=0,\\G(x,y,z)=0\end{matrix}}}$

s'appelle une courbe 3d implicite.

Un point ${\displaystyle (x_{0},y_{0},z_{0})}$ de la courbe est dit régulier si le produit vectoriel des gradients de ${\displaystyle F}$ et ${\displaystyle G}$ n'est pas nul en ce point:

${\displaystyle \mathbf {t} (x_{0},y_{0},z_{0})=\operatorname {grad} F(x_{0},y_{0},z_{0})\land \operatorname {grad} G(x_{0},y_{0},z_{0})\neq (0,0,0);}$

sinon il est dit singulier. Le vecteur ${\displaystyle \mathbf {t} (x_{0},y_{0},z_{0})}$ est un vecteur tangent à la courbe au point ${\displaystyle (x_{0},y_{0},z_{0}).}$

Exemples :

${\displaystyle (1)\quad x+y+z-1=0\ ,\ x-y+z-2=0}$

est une droite.

${\displaystyle (2)\quad x^{2}+y^{2}+z^{2}-4=0\ ,\ x+y+z-1=0}$

est une section plane de sphère, donc un cercle.

${\displaystyle (3)\quad x^{2}+y^{2}-1=0\,,x+y+z-1=0}$

est une ellipse (section plane d'un cylindre).

${\displaystyle (4)\quad x^{2}+y^{2}+z^{2}-16=0\,,(y-y_{0})^{2}+z^{2}-9=0}$

est la courbe d'intersection entre une sphère et un cylindre.

Pour le calcul des points de la courbe et sa visualisation, voir l'article Intersection.

Voir également

• Surface implicite

Références

• (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Implicit curve » (voir la liste des auteurs).
• Gomes, A., Voiculescu, I., Jorge, J., Wyvill, B., Galbraith, C.: Implicit Curves and Surfaces: Mathematics, Data Structures and Algorithms, 2009, Springer-Verlag London, (ISBN 978-1-84882-405-8)
• C:L : Bajaj, CM Hoffmann, RE Lynch : Tracing surface intersections, Comp. Aided Geom. Design 5 (1988), 285-307.
• Geometry and Algorithms for COMPUTER AIDED DESIGN

Liens externes

• Robert Ferréol, « Courbes 2D », sur Encyclopédie des formes mathématiques remarquables

• Portail des mathématiques