Cardioïde

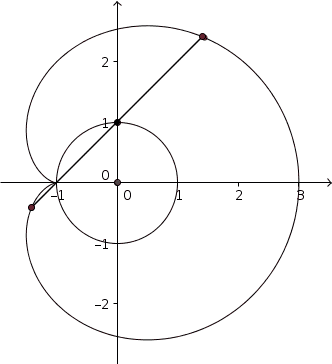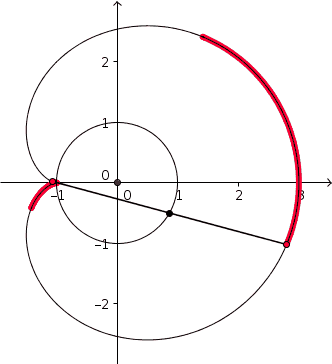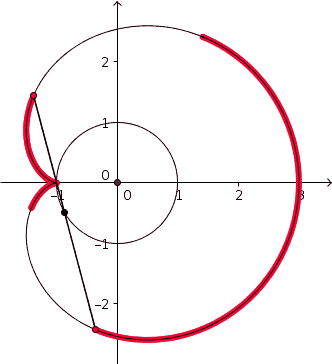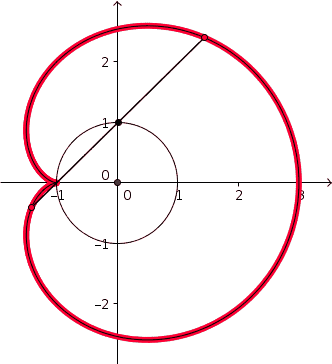
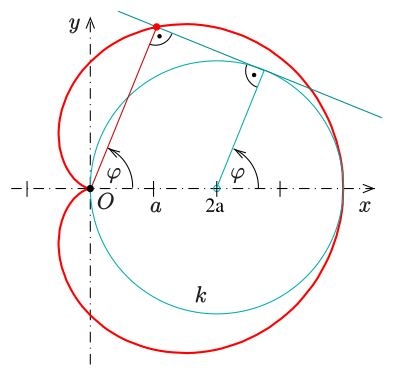
La cardioïde est une courbe algébrique plane, trajectoire d'un point fixé à un cercle qui roule sans glisser sur un second cercle de même diamètre. Il s'agit donc d'une courbe cycloïdale dont la directrice est un cercle (ou épicycloïde).

Étymologie et histoire

Son nom vient du grec kardia (cœur), en référence à sa forme, et lui fut donné par Jean Castillon.

D'abord étudiée comme un cas particulier du limaçon de Pascal, la première évocation de la cardioïde en tant qu'épicycloïde remonte à 1674 : Rømer l'étudia au cours de ses recherches sur la forme la plus adaptée aux dents des engrenages. En 1708, La Hire détermina son périmètre (8 fois le diamètre du cercle directeur). Castillon la décrit plus en détail et la baptisa dans un document qu'il publia en 1741. Néanmoins, comme il s'agit d'un cas particulier de limaçon de Pascal (courbe étudiée par Étienne Pascal, le père de Blaise), on peut dire que son histoire commence bien avant les travaux de La Hire et Castillon.

Définition analytique

La courbe peut être définie par l'équation cartésienne suivante :

${\displaystyle (x^{2}+y^{2}-ax)^{2}=a^{2}(x^{2}+y^{2})}$.

On peut également la définir par une équation polaire :

${\displaystyle \rho (\theta )=a(1+\cos \theta )}$

ou par une équation paramétrique :

${\displaystyle \left\{{\begin{matrix}x(\theta )=a\cos \theta (1+\cos \theta )\\y(\theta )=a\sin \theta (1+\cos \theta )\end{matrix}}\right.}$

Propriétés et applications

Géométrie

La cardioïde est :

• une conchoïde de cercle relativement à un point situé sur le cercle, avec une raison égale au diamètre du cercle. Il s'agit donc d'un cas particulier de limaçon de Pascal ;
• une podaire de cercle par rapport à l'un de ses points ;
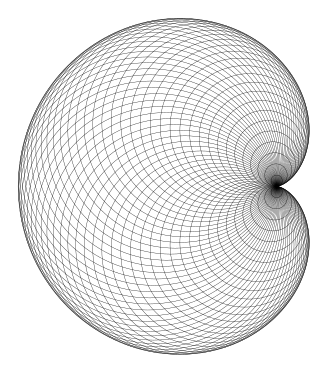
• l'enveloppe des cercles dont le centre décrit un cercle donné (C), et qui passent par un point donné A de ce cercle (C) ;
• une inverse de parabole par rapport à son foyer.
• dans le plan complexe, l'image du cercle de centre 1 et de rayon 1 par la fonction ${\displaystyle z\to z^{2}}$.

Le périmètre d'une cardioïde formée à partir d'un cercle de diamètre ${\displaystyle a\,}$ vaut ${\displaystyle 8a\,}$ ; son aire vaut ${\displaystyle {\frac {3}{2}}\pi a^{2}}$.

Comme pour toute courbe cycloïdale, la développée de la cardioïde est une cardioïde homothétique.

Optique

La cardioïde est une caustique de cercle par réflexion avec la source lumineuse située sur le cercle. Cette propriété explique que la forme dessinée au fond d'un récipient par la réflexion des rayons lumineux provenant d'une source ponctuelle proche du bord du récipient soit une cardioïde.

Lorsque la source est infiniment éloignée et que ce sont des rayons parallèles qui se reflètent sur le cercle, on distingue une forme comparable mais il s'agit alors d'une autre épicycloïde, la néphroïde.

La caustique par réflexion de la cardioïde, avec la source lumineuse au point de rebroussement de la cardioïde, est également une néphroïde.

Microphones à directivité cardioïde

On dit d'un microphone qu'il est unidirectionnel ou cardioïde lorsque sa sensibilité varie en fonction de la position de la source par rapport à l'axe du micro en dessinant une courbe en forme de cœur. Cette directivité s'obtient en ajoutant une directivité en huit (bidirectionnelle) à une directivité omnidirectionnelle :

• micro omnidirectionnel (capteur de pression) : ${\displaystyle {\overline {U}}=1}$ ;
• micro bidirectionnel (capteur de gradient de pression : ${\displaystyle {\overline {U}}=\cos \theta }$ ;
• micro cardioïde (capteur mixte) : ${\displaystyle {\overline {U}}=1+\cos \theta }$.

Le son provenant de l'arrière est complètement éliminé, celui venant des côtés, atténué. En dirigeant le micro vers la source, on réduit l'importance du son réverbéré, qui vient de toutes les directions. En sonorisation, on évite l'oscillation (effet Larsen) en plaçant les haut-parleurs de retour à l'arrière des micros.

On construit des microphones de directivité cardioïde large, supercardioïde et hypercardioïde en changeant les proportions entre la composante omnidirectionnelle et la composante bidirectionnelle.

Divers

On trouve une cardioïde au centre d'une fractale très connue, l'ensemble de Mandelbrot.

Notes et références

Cette section est vide, insuffisamment détaillée ou incomplète. Votre aide est la bienvenue ! Comment faire ?

Voir aussi

Articles connexes

• Cycloïde
• Néphroïde

Liens externes

• Notices dans des dictionnaires ou encyclopédies généralistes :

  • Den Store Danske Encyklopædi
  • Larousse
  • Store norske leksikon
• Notices d'autorité :

  • LCCN
  • Israël
• « Cardioïde », sur mathcurve.com

• Portail de la géométrie