Birapport

Le birapport, ou rapport anharmonique selon la dénomination de Michel Chasles est un outil puissant de la géométrie, en particulier la géométrie projective. La notion remonte à Pappus d'Alexandrie, mais son étude systématique est réalisée en 1827 par Möbius^[1].

Birapport de quatre points alignés

Définition élémentaire

Si A, B, C et D sont quatre points distincts d'une droite (d), le birapport, ou rapport anharmonique de ces quatre points est formé à partir des rapports des mesures algébriques des segments qu'ils découpent de la manière suivante :

${\displaystyle r=(A,B,C,D)={\frac {\frac {\overline {\mathrm {CA} }}{\overline {\mathrm {CB} }}}{\frac {\overline {\mathrm {DA} }}{\overline {\mathrm {DB} }}}}}$

Définir des mesures algébriques demande ordinairement d'introduire un repère sur la droite (d) ; mais les rapports de mesures algébriques sont en fait indépendants du repère introduit. La notion de birapport a donc un sens en géométrie affine, c'est-à-dire sans référence à une structure euclidienne. Si on utilise des unités de longueur, le birapport est une grandeur indépendante du choix d'unité.

Il n'existe pas de notation universelle pour le birapport : on trouve par exemple les écritures ${\displaystyle (A,B,C,D),[A,B,C,D],{\big [}\!|A,B,C,D|\!{\big ]}}$.

Influence de l'ordre des points

De par son expression, le birapport vérifie un certain nombre de propriétés de symétrie lorsqu'on permute les points : échanger A et B d'une part, C et D d'autre part est sans effet. De même si on échange le couple (A, B) et le couple (C, D). On peut donc considérer le birapport comme attaché à la paire de paires ${\displaystyle \{\{A,B\},\{C,D\}\}}$.

Lorsqu'on ne précise pas l'ordre des points sur la droite, selon les permutations, le birapport ne prend pas 4! = 24 valeurs mais seulement six^[2] : ${\displaystyle ~r;1-r;{\frac {1}{r}};{\frac {1}{1-r}};1-{\frac {1}{r}};{\frac {1}{1-{\frac {1}{r}}}}}$

Les fonctions correspondantes (telles que ${\displaystyle f_{4}:r\mapsto {\frac {1}{1-r}}}$) forment un groupe isomorphe au groupe symétrique ${\displaystyle {\mathfrak {S}}_{3}}$. Cela s'explique de la façon suivante : les permutations (autre que l'identité) qui laissent le birapport invariant sont

${\displaystyle (AB)(CD)\quad (AC)(BD)\quad (AD)(BC)}$

(on les a notées par leur décomposition en produit de cycles à support disjoints). Elles forment un sous-groupe normal de ${\displaystyle {\mathfrak {S}}_{4}}$, isomorphe au groupe de Klein, et le groupe des valeurs du birapport est donc le groupe quotient de ${\displaystyle {\mathfrak {S}}_{4}}$ par ce sous-groupe normal.

Propriétés

Le birapport reste invariant pour de nombreuses transformations géométriques : isométries, similitudes, transformations affines.

Si C est le barycentre de (A, a) et (B, b) et si D est celui de (A, a') et (B, b') alors le birapport de (A, B ; C, D) vaut ${\displaystyle {\frac {ab'}{a'b}}}$, ce qui justifie qu'une transformation affine, conservant les barycentres, conserve aussi les birapports.

Plus généralement, la propriété fondamentale est en fait l'invariance par la projection centrale, appelée aussi projection conique, ou perspective linéaire classique, centrale : quatre points d'une droite ont pour image quatre points de même birapport sur une autre droite. En conséquence, les homographies de la droite (d), qu'on peut obtenir à l'aide de telles projections, conservent le birapport.

Définition projective

L'invariance du birapport par projection centrale témoigne du fait qu'il s'agit d'un objet relevant en réalité de la géométrie projective. Le passage de droites affines à des droites projectives se fait intuitivement en ajoutant une notion de "point à l'infini". Les applications "naturelles" entre les droites projectives sont les homographies.

Plusieurs auteurs utilisent ainsi les homographies pour donner directement une définition plus générale du birapport : si A, B, C sont trois points distincts d'une droite projective (d), il existe une unique homographie de (d) sur la droite ${\displaystyle \mathbb {P} ^{1}(K)}$ qui envoie respectivement A, B, C sur ${\displaystyle \infty ,0,1}$. L'image du quatrième point, D, est alors appelée birapport de ces quatre points. Dans le cas du corps des réels, lorsqu'on effectue le calcul en coordonnées affines, on retombe sur la définition initiale, du moins pour des points qui ne sont pas à l'infini^[3],[4].

Avec cette définition, le birapport caractérise en fait l'existence d'une correspondance homographique : si A, B, C, D sont quatre points d'une droite projective, avec A, B, C distincts et si A', B', C', D' sont eux aussi quatre points d'une droite projective, les trois premiers étant distincts, il existe une homographie envoyant les uns sur les autres si et seulement s'il y a égalité des birapports. Une telle homographie est alors unique.

Birapport de quatre droites concourantes

Un résultat important en géométrie projective stipule qu'une projection centrale conserve le birapport. Il permet de dire dans la figure ci-jointe que les birapports de (A, B ; C, D) et (A', B' ; C', D') sont égaux quelles que soient les droites qui portent la série des quatre points. (Une démonstration est réalisable en utilisant plusieurs fois le théorème de Thalès).

Puisque ce rapport est indépendant de la sécante aux quatre droites, ce rapport ne dépend que de la position relative des quatre droites. Il est alors appelé birapport de ces quatre droites^[5]

${\displaystyle (d_{\mathrm {A} },d_{\mathrm {B} };d_{\mathrm {C} },d_{\mathrm {D} })}$

On montre, en fait, que ce rapport est égal à ${\displaystyle {\frac {\frac {\sin {\mathrm {COA} }}{\sin {\mathrm {COB} }}}{\frac {\sin {\mathrm {DOA} }}{\sin {\mathrm {DOB} }}}}}$, ce qui explique que le birapport soit indépendant de la transversale choisie.

La dualité par pôles et polaires réciproques conserve le rapport anharmonique de quatre éléments d'une structure unidimensionnelle.

Division harmonique

Lorsque le birapport est égal à -1, on dit que les quatre points sont en division harmonique. Le point D est alors appelé le conjugué de C par rapport à A et B. Les propriétés du birapport font que C est aussi le conjugué de D par rapport à ces mêmes points, et en sens inverse A et B sont conjugués par rapport à C et D. Le nom de rapport anharmonique autrefois donné au birapport provient de ce qu'il mesure le défaut du caractère harmonique d'un quadruplet de points alignés, le caractère harmonique pouvant être caractérisé par exemple uniquement par des propriétés d'incidence.

Exemple 1: la suite harmonique

Le point d'abscisse ${\displaystyle {\frac {1}{3}}}$ est le conjugué du point d'abscisse 1 par rapport aux points d'abscisse 0 et ${\displaystyle {\frac {1}{2}}}$.

le point d'abscisse ${\displaystyle {\frac {1}{4}}}$ est le conjugué de celui d'abscisse ${\displaystyle {\frac {1}{2}}}$ par rapport aux points d'abscisse 0 et ${\displaystyle {\frac {1}{3}}}$.

De manière générale, le point d'abscisse ${\displaystyle {\frac {1}{n+2}}}$ est le conjugué du point d'abscisse ${\displaystyle {\frac {1}{n}}}$ par rapport aux points d'abscisse ${\displaystyle {\frac {1}{n+1}}}$ et 0

On définit ainsi la suite de nombres ${\displaystyle 1,{\frac {1}{2}},{\frac {1}{3}},{\frac {1}{4}}}$… appelée suite harmonique que l'on retrouve en musique pour définir la gamme harmonique

Exemple 2 : moyenne harmonique

Le conjugué de 0 par rapport à x et y est la moyenne harmonique de x et de y :

${\displaystyle {\frac {2}{{\frac {1}{x}}+{\frac {1}{y}}}}}$

Exemple 3 : barycentre

Si C est le barycentre de (A, a) et (B, b) alors son conjugué par rapport à A et B est le barycentre de (A, -a) et (B, b)

Pour d'autres exemples :

Birapport de longueurs, d'aires et angles

En géométrie affine, le birapport ne s'exprime pas qu'en termes de mesure algébrique, mais aussi en termes d'aire algébrique, et en géométrie euclidienne, en termes d'angle orienté. Par exemple sur le schéma ci-contre l'aire des divers triangles peuvent s'exprimer de deux manières.

Par exemple pour OAB on a

${\displaystyle {\frac {1}{2}}\times \mathrm {OH} \times \mathrm {AB} ={\frac {1}{2}}\times \mathrm {OA} \times \mathrm {OB} \times \sin({\widehat {\mathrm {AOB} }})}$.

D'où, après simplifications de OH² ou de OA×OB×OC×OD, l'égalité des trois birapports : de longueurs, d'aires et de sinus.

Birapport sur un cercle

La propriété du birapport des sinus a une conséquence pour six points cocycliques A, B, C, D, M, P. Les angles ${\displaystyle {\widehat {\mathrm {AMB} }}}$ et ${\displaystyle {\widehat {\mathrm {APB} }}}$ étant égaux ou supplémentaires, leurs sinus sont égaux. Le birapport des droites M(ABCD) est égal à celui des droites P(ABCD). En conséquence on peut parler du birapport de 4 points sur un cercle. On démontre, sans les sinus, en géométrie projective que cette propriété est vraie pour une conique quelconque (étant donné une conique, si ABCDM sont fixes et si P parcourt la conique, alors le birapport des droites P(ABCD) est constant).

• 
  Birapport dans un cercle
• 
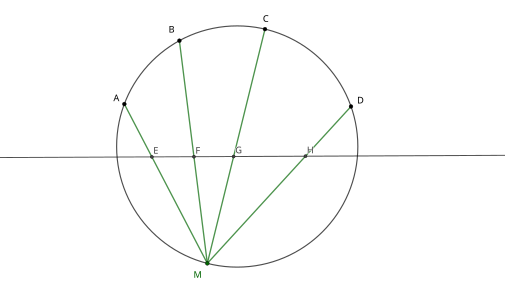  Inversion et rapport anharmonique dans un cercle

On peut en déduire que l'inversion de quatre points alignés, EFGH, de centre M, conserve leur birapport sur leurs images cocycliques ABCD.

Division harmonique, théorèmes de Ceva et de Ménélaüs

Le théorème de Ceva et le théorème de Ménélaüs sont reliés par un rapport harmonique.

Les deux théorèmes impliquent deux relations :

${\displaystyle {\frac {\overline {\mathrm {BD} }}{\overline {\mathrm {DC} }}}\cdot {\frac {\overline {\mathrm {CE} }}{\overline {\mathrm {EA} }}}\cdot {\frac {\overline {\mathrm {AF} }}{\overline {\mathrm {FB} }}}=1}$ et ${\displaystyle {\frac {\overline {\mathrm {D'B} }}{\overline {\mathrm {D'C} }}}\cdot {\frac {\overline {\mathrm {EC} }}{\overline {\mathrm {EA} }}}\cdot {\frac {\overline {\mathrm {FA} }}{\overline {\mathrm {FB} }}}=1}$.

qui, après simplification, mènent à :

${\displaystyle {\frac {\frac {\overline {\mathrm {DB} }}{\overline {\mathrm {DC} }}}{\frac {\overline {\mathrm {D'B} }}{\overline {\mathrm {D'C} }}}}=-1}$,

ce qui exprime que les points D et D' divisent le segment [BC] selon une division harmonique.

En passant cette propriété donne une construction du conjugué de D par rapport à BC, en prenant un point arbitraire A hors de (BC) et un point arbitraire M sur (AD).

Complexes

Déf : Soient α, β, γ et δ des complexes deux à deux distincts. On définit leur birapport ${\displaystyle [\alpha ,\beta ,\gamma ,\delta ]={\frac {(\alpha -\gamma )(\beta -\delta )}{(\alpha -\delta )(\beta -\gamma )}}\cdot }$

Prop : Quatre points (d'affixes) α, β, γ et δ sont cocycliques ou alignés ssi [α, β, γ, δ] ∈ ℝ.

Prop : Il existe une relation de Chasles multiplicative dans l'ensemble des birapports mettant en jeu cinq nombres a, b, c, d et e. ${\displaystyle [a,b,c,d]\times [a,b,d,e]=[a,b,c,e]}$. Les nombres a et b ne changent pas, le nombre d sert d'intermédiaire entre c et e. Un simple développement de l'expression permet de la vérifier.

Prop : on trouvera dans Géométrie analytique classique, cité en bibliographie, la spectaculaire « formule des six birapports » énoncée par Daniel Perrin.

Définition via l'algèbre linéaire

On considère dans un espace vectoriel ${\displaystyle E}$ de dimension deux -autrement dit un plan vectoriel-, quatre droites vectorielles distinctes ${\displaystyle D_{1},D_{2},D_{3}{\text{ et }}D}$. Il existe alors trois vecteurs ${\displaystyle \neq 0,x_{1}\in D_{1},x_{2}\in D_{2},x_{3}\in D_{3}{\text{ tels que }}x_{3}=x_{1}+x_{2}}$, et ces vecteurs sont déterminés à un facteur scalaire ${\displaystyle \neq 0}$ près. Il existe alors un scalaire et un seul ${\displaystyle \rho }$ tel que ${\displaystyle x_{1}+\rho x_{2}\in D}$ ; on dit que ${\displaystyle \rho }$ est le birapport du quadruplet ${\displaystyle (D_{1},D_{2},D_{3},D)}$^[6],[7].

Bibliographie

• Jean-Denis Eiden, Géométrie analytique classique, Calvage & Mounet, 2009, 508 p. (ISBN 978-2-916352-08-4)
• Bruno Ingrao, Coniques projectives, affines et métriques : cours et exercices, Paris, Calvage & Mounet, 2011, 355 p. (ISBN 978-2-916352-12-1)
• Daniel Perrin, « Géométrie projective plane et applications aux géométries euclidienne et non euclidiennes », livre en préparation (consulté le 27 décembre 2018)

Notes et références

• Portail de la géométrie