Algorithme de Dinic

L'algorithme de Dinic ou algorithme de Dinitz est un algorithme en temps polynomial (et même fortement polynomial^[1]) de calcul du flot maximum dans un réseau, publié en 1970 par Yefim Dinitz^[2]. Le temps de calcul est en ${\displaystyle O(|V|^{2}|E|)}$ pour un graphe dont ${\displaystyle V}$ est l'ensemble des sommets et ${\displaystyle E}$ l’ensemble des arcs. Il est semblable à l'algorithme d'Edmonds-Karp dont le temps d'exécution est en ${\displaystyle O(|V||E|^{2})}$. Comme lui, il utilise des chemins augmentants de longueur minimale. L'introduction des concepts de graphe de niveau et de flot bloquant permet d'obtenir cette meilleure performance.

Définitions

Soit ${\displaystyle G=((V,E),c,s,t)}$ un réseau; ${\displaystyle c(u,v)}$ et ${\displaystyle f(u,v)}$ dénotent respectivement la capacité et le flot sur un arc ${\displaystyle (u,v)}$.

La capacité résiduelle est l’application ${\displaystyle c_{f}:V\times V\to R^{+}}$ définie comme suit :

• si ${\displaystyle (u,v)\in E}$,

  ${\displaystyle c_{f}(u,v)=c(u,v)-f(u,v)}$,

  ${\displaystyle c_{f}(v,u)=f(u,v)}$,

• ${\displaystyle c_{f}(u,v)=0}$ sinon.

Le graphe résiduel est le graphe ${\displaystyle G_{f}=((V,E_{f}),c_{f}|_{E_{f}},s,t)}$, où

${\displaystyle E_{f}=\{(u,v)\in V\times V:c_{f}(u,v)>0\}}$.

Un chemin augmentant est un chemin de la source ${\displaystyle s}$ au puits ${\displaystyle t}$ (on dit aussi un ${\displaystyle s}$-${\displaystyle t}$-chemin) dans le graphe résiduel. On note ${\displaystyle d(v)}$ la longueur des plus courts chemins de la source ${\displaystyle s}$ au sommet ${\displaystyle v}$ dans ${\displaystyle G_{f}}$ (${\displaystyle d(v)}$ est la distance de la source à ${\displaystyle v}$).

Le graphe de niveau de ${\displaystyle G_{f}}$ est le graphe ${\displaystyle G_{L}=(V,E_{L},c_{f}|_{E_{L}},s,t)}$, où

${\displaystyle E_{L}=\{(u,v)\in E_{f}:d(v)=d(u)+1\}}$.

En d'autres termes, c'est le sous-graphe contenant uniquement les arcs qui relient un sommet à un sommet de distance immédiatement supérieure.

Un flot bloquant est un flot ${\displaystyle f}$ tel que le graphe ${\displaystyle G'=(V,E_{L}',s,t)}$ avec ${\displaystyle E_{L}'=\{(u,v):f(u,v)<c_{f}|_{E_{L}}(u,v)\}}$ obtenu en ne conservant que les arcs sur lesquels le flot ${\displaystyle f}$ est strictement inférieur à la capacité ${\displaystyle c_{f}|_{E_{L}}}$ ne contient aucun ${\displaystyle s}$-${\displaystyle t}$-chemin. Autrement dit, un flot est bloquant si tout ${\displaystyle s}$-${\displaystyle t}$-chemin contient un arc où le flot est égal à la capacité.

L'Algorithme

Algorithme de Dinic

Entrée: Un réseau ${\displaystyle G=((V,E),c,s,t)}$.

Sortie: Un flot ${\displaystyle f}$ de valeur maximale.

1. Poser ${\displaystyle f(u,v)=0}$ pour tout ${\displaystyle (u,v)\in E}$.
2. Construire le graphe de niveau ${\displaystyle G_{L}}$ de ${\displaystyle G_{f}}$ à partir de ${\displaystyle G}$. Si le puits n'est pas accessible, terminer et retourner le flot ${\displaystyle f}$.
3. Déterminer un flot bloquant ${\displaystyle f\;'}$ dans ${\displaystyle G_{L}}$.
4. Augmenter le flot ${\displaystyle \ f}$ de ${\displaystyle f\;'}$ et retourner au point 2.

Exemple

L'exemple suivant montre l'exécution de l'algorithme de Dinic. Dans le graphe de niveau ${\displaystyle G_{L}}$ les valeurs en rouge sont les distances à la source, les arcs en bleu forment un flot bloquant.

	${\displaystyle G}$	${\displaystyle G_{f}}$	${\displaystyle G_{L}}$
1.
	Au départ, le flot est nul, donc ${\displaystyle G_{f}=G}$. Le flot bloquant obtenu à la fin de la première étape a pour valeur 14. Il est composé de trois chemins augmentant, tous de longueur 3. Ce sont ${\displaystyle \{s,1,3,t\}}$ avec valeur 4, ${\displaystyle \{s,1,4,t\}}$ avec valeur 6, ${\displaystyle \{s,2,4,t\}}$ avec valeur 4.
2.
	Le graphe résiduel ${\displaystyle G_{f}}$ a des arcs opposés à ceux du graphe de départ, notamment lorsque la capacité est égale au flot. Les distances ne sont plus les mêmes. Le flot bloquant a pour valeur 5. Il correspond au chemin seul augmentant ${\displaystyle \{s,2,4,3,t\}}$ avec valeur 5. La valeur du flot devient 14 + 5 = 19. Le chemin augmentant est composé de 4 arcs.
3.
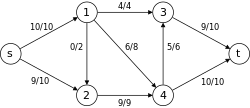
	Le sommet ${\displaystyle t}$ n'est plus accessible dans ${\displaystyle G_{f}}$. L'algorithme se termine et retourne un flot dont la valeur est 19. Notons que dans chaque flot bloquant, le nombre d'arcs du chemin augmentant croît d'au moins 1.

Analyse

Cas général

On peut montrer que le nombre d'arcs dans chaque flot bloquant croit d'au moins 1 à chaque étape; il y a donc au plus ${\displaystyle n-1}$ étapes, et au plus ${\displaystyle n-1}$flots bloquants à calculer, où ${\displaystyle n}$ est le nombre de sommets du réseau.

Le graphe de niveau ${\displaystyle G_{L}}$ peut être calculé par un parcours en largeur; un tel parcours prend un temps en ${\displaystyle O(m)}$, où ${\displaystyle m}$ est le nombre d'arcs. Un flot bloquant peut être calculé en temps ${\displaystyle O(nm)}$ . Le temps total de l'algorithme de Dinic est donc en ${\displaystyle O(n^{2}m)}$.

On peut diminuer le temps de calcul d'un flot bloquant en utilisant une structure de données de la famille des arbres dynamiques, soit les arbres adaptatifs (self-adjusting trees) soit les link/cut tree (en), inventés par Sleator et Tarjan. La détermination du flot bloquant de chaque étape peut être ramenée à ${\displaystyle O(m\log n)}$, et le temps total à ${\displaystyle O(nm\log n)}$.

Cas particuliers

Capacités 0 ou 1. Dans un réseau où les capacités sont 0 ou 1, la complexité en temps peut être nettement mieux bornée. Chaque flot bloquant peut être trouvé en temps ${\displaystyle O(m)}$, et on peut montrer que, de plus, le nombre d'étapes est majoré par ${\displaystyle O({\sqrt {m}})}$ et ${\displaystyle O(n^{2/3})}$. L'algorithme est donc en temps ${\displaystyle O(\min(n^{2/3},m^{1/2})m)}$.

Réseaux de couplages. Dans les réseaux qui interviennent dans la résolution du couplage biparti, le nombre de phases est borné par ${\displaystyle O({\sqrt {n}})}$, ce qui donne un temps borné par ${\displaystyle O({\sqrt {n}}m)}$. L'algorithme est aussi connu sous le nom d'algorithme de Hopcroft-Karp.

Réseaux unitaires. Plus généralement, cette borne reste valable pour des réseaux dits unitaires, qui sont des réseaux où chaque sommet autre que la source et le puits possèdent soit un arc entrant de capacité un, soit un arc sortant de capacité un, les autres arcs ayant des capacités qui sont des entiers arbitraires^[3].

Historique

Dinic ou Dinitz ?

L'algorithme de Dinic a été publié en 1970 par Yefim (Chaim) A. Dinitz (Ефим Диниц), alors qu'il était en Russie. Comme le dit Dinitz dans son article historique en hommage au mathématicien et informaticien Shimon Even, le rideau de fer séparait alors efficacement les chercheurs soviétiques des autres; son algorithme a été traduit dans la même année, et dans cette traduction, la lettre finale de son nom est remplacée par un « c ». C'est Shimon Even et Alon Itai, alors élève d'Even, qui ont découvert la traduction assez obscure de l'article, lui ont apporté des modifications et compléments, et en ont répandu la connaissance dans le monde scientifique occidental. Dinitz dit que l'algorithme ainsi reformulé - et qui circule encore aujourd'hui sous le nom d'algorithme de Dinic - doit son succès à Even et Atai, et que son algorithme original, algorithme de Dinitz, n'aurait peut-être pas eu ce succès. L'algorithme continue à être appelé algorithme de Dinic dans les ouvrages de référence^[4], et par Dinitz lui-même, sur un ton amusé^[5]. Dinitz est maintenant membre du département d'informatique de l’université Ben Gourion du Néguev en Israël^[6]. Ses publications scientifiques paraissent toujours sous son vrai nom.

Dinic et Edmonds-Karp

Deux ans plus tard, en 1972, paraît l'algorithme d'Edmonds-Karp mais qui avait déjà été présenté plus tôt^[7]. Ils ont montré indépendamment que si l'on choisit comme chemin augmentant le plus court à chaque pas, alors la longueur des chemins augmentant est croissante au sens large. L'algorithme est moins efficace que celui de Dinic parce qu'il ne fait pas usage de la notion de distance. Il avait déjà été présenté à une conférence aux États-Unis en 1968 (donc avant la publication de l'article de Dinic), mais pas publié à l'époque.

Articles connexes

• Algorithme de Ford-Fulkerson
• Problème de flot maximum

Notes

Bibliographie

• E. A. Dinic, « Algorithm for solution of a problem of maximum flow in a network with power estimation », Soviet Math. Doklady, Doklady Nauk SSSR, vol. 11,‎ 1970, p. 1277–1280 (lire en ligne). Traduction anglaise de l’article russe paru la même année.
• Yefim Dinitz, « Dinitz' Algorithm: The Original Version and Even's Version », dans Oded Goldreich, Arnold L. Rosenberg et Alan L. Selman, Theoretical Computer Science: Essays in Memory of Shimon Even, Springer, 2006 (ISBN 978-3-540-32880-3, lire en ligne), p. 218–240
• Robert E. Tarjan, Data structures and network algorithms, 1983
• (en) Bernard H. Korte et Jens Vygen, Combinatorial Optimization : Theory and Algorithms, Springer, coll. « Algorithms and Combinatorics » (n^o 21), 2008, 627 p. (ISBN 978-3-540-71844-4), « 8.4 Blocking Flows and Fujishige's Algorithm », p. 174–176

Traduction française:

• Bernard Korte, Jens Vygen et Jean Fonlupt et Alexandre Skoda (traducteurs), Optimisation combinatoire : théorie et algorithmes, Springer-France, coll. « IRIS », 2010 (ISBN 978-2-287-99036-6), « 8.4 Flots bloquants et algorithme de Fujishige », p. 180–182
• (en) Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest et Clifford Stein, Introduction to Algorithms, Cambridge, MIT Press and McGraw-Hill, 2001, 2^e éd., 1180 p. (ISBN 978-0-262-53196-2, LCCN 2001031277), chap. 26 (« Chap. 26 Flows »), p. 643–700. Traduction française : Introduction à l'algorithmique, 2^e édition, Dunod 2002, « chapitre 26. Flot Maximum ».

• Portail de l'informatique théorique
• Portail des mathématiques